חוק אוהם למעגל מגנטי

אם לא היו שטפים מגנטיים, לא סביר שהנדסת חשמל מודרנית הייתה קיימת. פעולתם של גנרטורים ומנועים חשמליים, אלקטרומגנטים ושנאים, מכשירי מדידה וחיישני הול מבוססת על השימוש בשדה המגנטי ובתכונות השטף המגנטי.

כדי לרכז ולחזק את השטף המגנטי, הם פונים לשימוש בחומרים פרומגנטיים. חומרים פרומגנטיים מיוצרים ליבות מגנטיות - גופים בצורות ובגדלים הנדרשים, ליבות להכוונת שטפים מגנטיים בגודל כזה או אחר לכיוון הנדרש. גופים כאלה, שבתוכם עוברים קווים סגורים של אינדוקציה מגנטית, נקראים מעגלים מגנטיים.

התכונות הידועות של השדה המגנטי מאפשרות לחשב את השטפים המגנטיים במעגלים מגנטיים שונים. אבל לעבודה מעשית הרבה יותר נוח לפנות להשלכות כלליות ולחוקים של מעגלים מגנטיים הנגזרים מחוקי השדה המגנטי, במקום להשתמש בחוקים אלו ישירות בכל פעם. החלת כללים מסוימים על מעגלים מגנטיים נוחה יותר לפתרון בעיות מעשיות טיפוסיות.

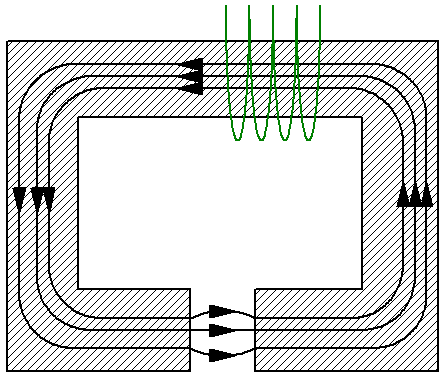
לדוגמה, שקול מעגל מגנטי פשוט המורכב מעול לא מסועף של חתך S, אשר בתורו עשוי מחומר עם חדירות mu... לעול יש פער לא מגנטי של אותו שטח S, למשל אוויר, והחדירות המגנטית במרווח - mu1 - שונה מהחדירות המגנטית של העול. כאן אתה יכול להסתכל על קו האינדוקציה הממוצע ולהחיל עליו את משפט המתח המגנטי:

מכיוון שקווי האינדוקציה המגנטית הם רציפים לאורך המעגל, גודל השטף המגנטי הן בעול והן בפער זהה. כעת אנו משתמשים בנוסחאות עבור אינדוקציה מגנטית B והשטף המגנטי F יבטא את עוצמת ה-H של השדה המגנטי במונחים של השטף המגנטי F.

השלב הבא הוא להחליף את הביטויים המתקבלים בנוסחה שלעיל של משפט השטף המגנטי:

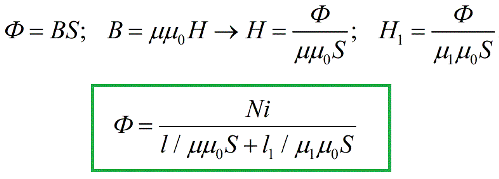
השגנו נוסחה דומה מאוד לזו המוכרת בהנדסת חשמל חוק אוהם לקטע של מעגל סגור, ואת תפקידו של ה-EMF כאן ממלאת הכמות iN, הנקראת הכוח המגנטו-מוטיבי (או MDF) באנלוגיה לכוח האלקטרו-מוטיבי. במערכת SI, כוח מגנטו-מוטיבי נמדד באמפר.

הסכום במכנה הוא לא יותר מאשר אנלוגיה של ההתנגדות החשמלית הכוללת למעגל חשמלי, ולמעגל מגנטי היא נקראת ההתנגדות המגנטית הכוללת בהתאם. המונחים במכנה הם ההתנגדויות המגנטיות של חלקים בודדים של המעגל המגנטי.

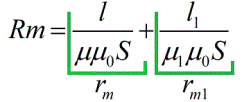
התנגדויות מגנטיות תלויות באורך המעגל המגנטי, בשטח החתך שלו ובחדירות המגנטית (בדומה למוליכות החשמלית לחוק אוהם הרגיל).כתוצאה מכך, אתה יכול לכתוב את הנוסחה של חוק אוהם, רק עבור מעגל מגנטי:

כלומר, הניסוח של חוק אוהם ביחס למעגל מגנטי נשמע כך: "במעגל מגנטי ללא הסתעפות, השטף המגנטי שווה למנה של חלוקת MDS בהתנגדות המגנטית הכוללת של המעגל."

ברור מהנוסחאות שההתנגדות המגנטית ב-NE נמדד באמפר וובר, וההתנגדות המגנטית הכוללת של מעגל מגנטי שווה מספרית לסכום ההתנגדויות המגנטיות של חלקי אותו מעגל מגנטי.

המצב המתואר תקף למעגל מגנטי לא מסועף הכולל כל מספר חלקים, בתנאי שהשטף המגנטי חודר ברציפות לכל החלקים הללו. אם הליבות המגנטיות מחוברות בסדרה, ההתנגדות המגנטית הכוללת נמצאת על ידי הוספת ההתנגדויות המגנטיות של החלקים.

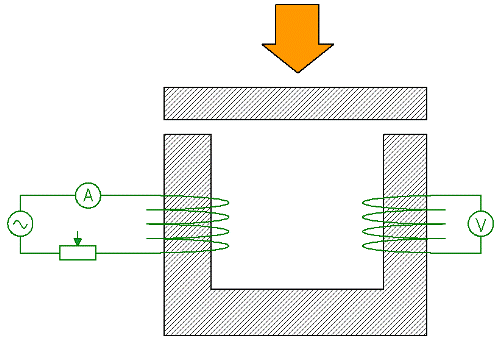
ראו כעת ניסוי המדגים את השפעת חוסר הרצונות של חלקי מעגל על ​​הסרבנות הכוללת של מעגל. מעגל מגנטי בצורת U ממוגנט על ידי סליל 1, המוזן (זרם חילופין) דרך מד זרם וראווסטט. EMF מושרה בפיתול המשנית 2, והקריאות של מד המתח המחובר לליפוף, כידוע, הן פרופורציונליות לשטף המגנטי במעגל המגנטי.

אם כעת תשאיר את הזרם בפיתול הראשוני ללא שינוי על ידי ויסותו באמצעות ריאוסטט, ובמקביל תלחץ על לוח הברזל כנגד המעגל המגנטי שלמעלה, לאחר שההתנגדות המגנטית הכוללת של המעגל תפחת מאוד, קריאת מד המתח יגדל בהתאם.

כמובן, המונחים לעיל, כגון "התנגדות מגנטית" ו"כוח מגנטו-מוטיבי", הם מושגים פורמליים, שכן שום דבר בשטף המגנטי לא זז, אין חלקיקים נעים, זה רק ייצוג חזותי (כמו מודל זרימת נוזלים) של הבנה ברורה יותר של החוקים...

המשמעות הפיזית של הניסוי הנ"ל ושל ניסויים דומים אחרים היא להבין כיצד הכנסת פערים לא מגנטיים וחומרים מגנטיים למעגל המגנטי משפיעה על השטף המגנטי במעגל המגנטי.

על ידי הכנסת, למשל, מגנט למעגל מגנטי, אנו מוסיפים זרמים מולקולריים נוספים לגופים שכבר מצויים במעגל, שמכניסים שטפים מגנטיים נוספים. מושגים פורמליים כגון "התנגדות מגנטית" ו"כוח מגנטו-מוטיבציה" מתגלים כנוחים מאוד בעת פתרון בעיה מעשית, וזו הסיבה שהם משמשים בהצלחה בהנדסת חשמל.