זרם אימפולס

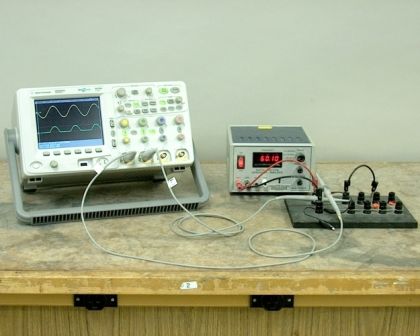
במכשירים אלקטרוניים שונים, למשל, בציוד אלקטרוני ומוליך למחצה, כלומר במגברים, מיישרים, מכשירי רדיו, גנרטורים, טלוויזיות, כמו גם במיקרופונים פחמן, טלגרפים והתקנים רבים אחרים, הם נמצאים בשימוש נרחב בזרמי גלים ומתחים... לא לחזור על הנימוק פעמיים, נדבר רק על זרמים, אבל כל מה שקשור לזרמים נכון גם למתחים.

זרמים פועמים בעלי כיוון קבוע אך משנים את ערכם יכולים להיות שונים. לפעמים הערך הנוכחי משתנה מהערך הגבוה ביותר לנמוך ביותר שאינו אפס. במקרים אחרים, הזרם מצטמצם לאפס. אם מעגל זרם ישר מופסק בתדר מסוים, אז במשך כמה מרווחי זמן אין זרם במעגל.

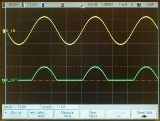
באיור. 1 מציג גרפים של זרמי גל שונים. באיור. 1, א, ב, השינוי בזרמים מתרחש לפי עקומה סינוסואידית, אך אין לראות בזרמים אלו לזרמי חילופין סינוסואידיים, שכן כיוון (סימן) הזרם אינו משתנה. באיור.1, c מראה זרם המורכב מפולסים נפרדים, כלומר "זעזועים" קצרי מועד של זרם, המופרדים זה מזה על ידי הפסקות באורך גדול או קטן יותר, ולעתים קרובות נקרא זרם פועם. זרמים פולסים שונים נבדלים זה מזה בצורתם ובמשך הפולסים, כמו גם בקצב החזרות.

נוח להתייחס לזרם פועם מכל סוג שהוא כסכום של שני זרמים - ישירים ומתחלפים, הנקראים זרמי מונח או רכיבים. לכל זרם פועם יש רכיבי DC ו-AC. זה נראה מוזר לרבים. למעשה, אחרי הכל, זרם פועם הוא זרם שזורם כל הזמן בכיוון אחד ומשנה את ערכו.

איך אתה יכול לדעת שהוא מכיל זרם חילופין שמשנה כיוון? עם זאת, אם שני זרמים - ישירים ומתחלפים - עוברים בו זמנית באותו חוט, מתברר שזרם פועם יזרום באותו חוט (איור 2). במקרה זה, המשרעת של זרם החילופין לא תעלה על הערך של הזרם הישר. זרמים ישירים וחילופין אינם יכולים לזרום בנפרד דרך החוט. הם מוסיפים לזרימה כללית של אלקטרונים שיש לה את כל התכונות של זרם פועם.

אורז. 1. גרפים של זרמי גל שונים

ניתן להציג את התוספת של זרמי AC ו-DC בצורה גרפית. באיור. 2 מציג את הגרפים של זרם ישר השווה ל-15 mA וזרם חילופין עם משרעת של 10 mA. אם נסכם את ערכי הזרמים הללו עבור נקודות זמן בודדות, תוך התחשבות בכיווני (סימנים) של הזרמים, נקבל את גרף זרם הגל המוצג באיור. 2 עם קו מודגש. זרם זה משתנה מנמוך של 5 mA לגבוה של 25 mA.

התוספת הנחשבת של זרמים מאשרת את תקפות הייצוג של הזרם הפועם כסכום של זרמים ישירים ומתחלפים. נכונות הייצוג הזה מאושרת גם על ידי העובדה שבעזרת מכשירים מסוימים ניתן להפריד את מרכיבי הזרם הזה זה מזה.

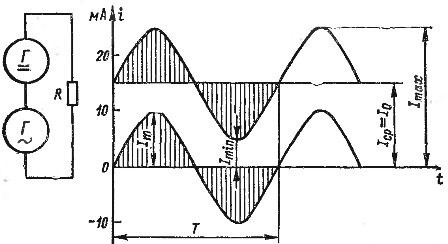
אורז. 2. השגת זרם פועם על ידי הוספת זרם ישר וחילופין.

יש להדגיש שכל זרם תמיד יכול להיות מיוצג כסכום של מספר זרמים. לדוגמה, זרם של 5 A יכול להיחשב כסכום של זרמים 2 ו-3 A הזורמים בכיוון אחד, או סכום של זרמים 8 ו-3 A הזורמים בכיוונים שונים, כלומר, במילים אחרות, ההבדל בין זרמים 8 ו-3 A. לא קשה למצוא שילובים אחרים של שני זרמים או יותר שנותנים סך של 5 A.

כאן יש דמיון מוחלט לעקרון החיבור והפירוק של כוחות. אם שני כוחות מכוונים בצורה שווה על עצם כלשהו, ​​ניתן להחליפם בכוח משותף אחד. ניתן להחליף כוחות הפועלים בכיוונים מנוגדים בהפרש יחידה. לעומת זאת, כוח נתון תמיד יכול להיחשב כסכום של כוחות תואמים מכוונים שווה או להפרש בין כוחות מכוונים הפוך.

אין צורך לפרק זרמי חילופין ישירים או סינוסואידים לזרמי רכיבים. אם נחליף את הזרם הפועם בסכום של זרמים ישרים וחילופין, אז על ידי החלת החוקים הידועים של זרמים ישירים וחילופין על זרמים רכיבים אלה, ניתן לפתור בעיות רבות ולבצע את החישובים הנדרשים הקשורים לזרם פועם.

הרעיון של זרם פועם כסכום של זרמים ישירים וחילופין הוא קונבנציונלי.כמובן, לא ניתן להניח שבמרווחי זמן מסוימים הזרמים הישירים והמתחלפים באמת זורמים זה לזה לאורך החוט. למעשה, אין שתי זרימות מנוגדות של אלקטרונים.

במציאות, זרם פועם הוא זרם יחיד המשנה את ערכו לאורך זמן. נכון יותר לומר שניתן לייצג את המתח הפועם או ה-EMF הפועם כסכום הרכיבים הקבועים והמשתנים.

לדוגמה, באיור. 2 מראה כיצד באופן אלגברי מתווסף ה-emf הקבוע של מחולל אחד ל-emf המשתנה של מחולל אחר. כתוצאה מכך, יש לנו EMF פועם שגורם לזרם הפועם המתאים. עם זאת, באופן מותנה, ניתן להתייחס לכך ש-EMF קבוע יוצר זרם ישר במעגל, ו-EMF לסירוגין - זרם חילופין, אשר בסיכום, יוצר זרם פועם.

ניתן לאפיין כל זרם פועם על ידי ערכי המקסימום והמינימום של Itax ואיטין, כמו גם מרכיביו הקבועים והמשתנים. הרכיב הקבוע מסומן ב-I0. אם הרכיב המתחלף הוא זרם סינוסואידי, אז המשרעת שלו מסומנת על ידי זה (כל הכמויות הללו מוצגות באיור 2).

אין לבלבל את זה עם It ו-Itax. כמו כן, הערך המקסימלי של הגל הנוכחי Imax לא צריך להיקרא משרעת. המונח משרעת מתייחס בדרך כלל רק לזרמי חילופין. לגבי הזרם הפועם, אנחנו יכולים לדבר רק על המשרעת של המרכיב המשתנה שלו.

הרכיב הקבוע של הזרם הפועם יכול להיקרא הערך הממוצע שלו Iav, כלומר הערך הממוצע האריתמטי. ואכן, אם ניקח בחשבון את השינויים בתקופה אחת של הזרם הפועם המוצג באיור.2, ניתן לראות בבירור את הדברים הבאים: בחצי המחזור הראשון, מספר ערכים מתווספים לזרם 15 mA על ידי שינוי רכיב הזרם, במשתנה מ-0 ל-10 mA ובחזרה ל-0, ובמחצית השנייה -מחזור, בדיוק אותם ערכי זרם מופחתים מהזרם 15 mA.

לכן, הזרם של 15 mA הוא באמת הערך הממוצע. מכיוון שזרם הוא העברת מטענים חשמליים דרך חתך החוט, אז Iav הוא הערך של זרם ישר כזה שבתקופה אחת (או במשך מספר שלם של תקופות) נושא את אותה כמות חשמל כמו הזרם הפועם הזה .

עבור זרם חילופין סינוסואידי, הערך של Iav לתקופה הוא אפס מכיוון שכמות החשמל שעברה בחתך המוליך בחצי תקופה אחת שווה לכמות החשמל העוברת בכיוון ההפוך במהלך חצי תקופה אחרת. בגרפים של זרמים המראים את תלות הזרם i בזמן t, כמות החשמל שנושא הזרם מתבטאת בשטח הדמות התחום על ידי עקומת הזרם, שכן כמות החשמל נקבעת על ידי מוצר שזה .

עבור זרם סינוסואידי, שטחי חצי הגלים החיוביים והשליליים שווים בזרם הפועם המוצג באיור. 2, במהלך המחצית הראשונה מתווספת כמות החשמל שנושא רכיב ה-AC לכמות החשמל שנושא ה-Iav הנוכחי (אזור מוצל באיור). ובמהלך חצי המחזור השני, בדיוק אותה כמות חשמל נמשכת. כתוצאה מכך, אותה כמות חשמל מועברת לאורך כל התקופה כמו עם זרם ישר Iav בודד, כלומר, שטח המלבן Iav T שווה לשטח התחום על ידי עקומת זרם הגל.

לפיכך, המרכיב הקבוע או הערך הממוצע של הזרם נקבע על ידי העברת מטענים חשמליים דרך חתך החוט.

המשוואה הנוכחית המוצגת באיור. ברור שצריך לכתוב את 2 בצורה הבאה:

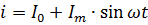
יש לחשב את הספק הזרם הפועם כסכום ההספקים של הזרמים המרכיבים אותו. לדוגמה, אם הזרם המוצג באיור. 2, עובר דרך נגד של התנגדות R, אז הכוח שלו הוא

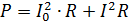
כאשר I = 0.7Im הוא ערך ה-rms של הרכיב המשתנה.

אתה יכול להציג את הרעיון של ערך ה-rms של זיהוי זרם הגל. הספק מחושב בדרך הרגילה:

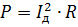
משווים את הביטוי הזה לקודם ומצמצמים אותו עם R, נקבל:

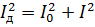
ניתן להשיג את אותם מערכות יחסים עבור מתחים.