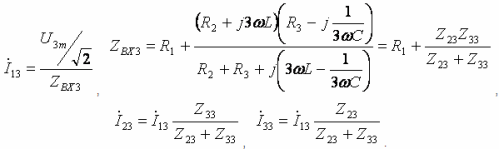מעגלים חשמליים עם זרם לא סינוסואידי

זרמים לא-סינוסואידים ופירוקם

במעגל חשמלי, זרמים לא-סינוסואידים יכולים להתרחש משתי סיבות:

1. המעגל החשמלי עצמו הוא ליניארי, אך מתח לא סינוסואידי פועל על המעגל,

2. המתח הפועל על המעגל הוא סינוסואידי, אך המעגל החשמלי מכיל אלמנטים לא ליניאריים.

יכולות להיות שתי הסיבות. פרק זה עוסק במעגלים עבור הנקודה הראשונה בלבד. במקרה זה, המתחים הלא-סינוסואידים נחשבים למחזוריים.

גנרטורים של פולסים תקופתיים משמשים במכשירים שונים של הנדסת רדיו, אוטומציה, טלמכניקה. צורת הפולסים יכולה להיות שונה: מסור, מדורג, מלבני (איור 1).

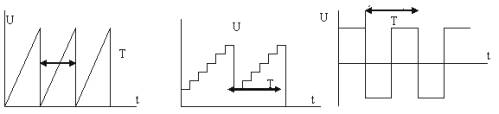
איור 1. צורות דופק

התופעות המתרחשות במעגל חשמלי ליניארי תחת מתחים מחזוריים אך לא-סינוסואידים הם הקלים ביותר למחקר אם עקומת המתח מורחבת בסדרת פורייה טריגונומטרית:

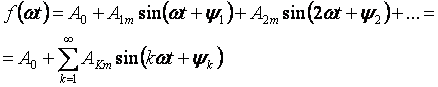
האיבר הראשון של הסדרה A0 נקרא הרכיב הקבוע או ההרמוני האפסי, האיבר השני של הסדרה

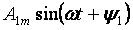
- ההרמונית הבסיסית או הראשונה וכל שאר איברי הצורה

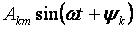
עבור k> 1 נקראות הרמוניות גבוהות יותר.

אם בביטוי (3.1) נפתח את הסינוס של הסכום, אז נוכל לעבור לצורה אחרת של כתיבת הסדרה:

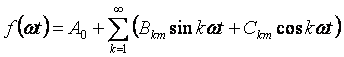אם הפונקציה סימטרית על ציר האבשיסה, הרי שהסדרה אינה מכילה רכיב קבוע. אם הפונקציה היא סימטרית על ציר האורדיטות, אז הסדרה לא מכילה סינוסים. הפונקציה סימטרית לגבי המקור ואינה מכילה קוסינוסים.

כמה דוגמאות להרחבת סדרות מובאות בטבלה. 1 והם זמינים גם בספרות ההתייחסות.

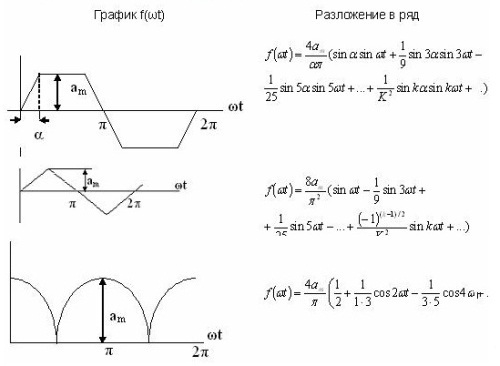
טבלה 1. הרחבת סדרת פורייה

חישוב מעגלי זרם לא-סינוסואידיים

המעגל מחושב עבור כל הרמונית לפי המודל. המעגל מחושב כמה פעמים שיש הרמוניות במתח הפועל על המעגל. במקרה זה, יש צורך לקחת בחשבון מספר מאפיינים.

יש לציין כי ההתנגדות של האלמנט האינדוקטיבי עולה ככל שהמספר ההרמוני עולה

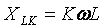
והאלמנט הקיבולי, להיפך, פוחת:

כמו כן יש לקחת בחשבון שהמרכיב הקבוע של הזרם אינו עובר דרך הקבל וההשראות אינה התנגדות אליו.

בנוסף, אין לשכוח את תופעות התהודה האפשריות לא רק בהרמונית היסודית, אלא גם בהרמוניות גבוהות יותר.

דיאגרמות וקטוריות ניתן לשרטט עבור כל הרמוניה בנפרד.

על פי עקרון הסופרפוזיציה, הזרם של כל ענף יכול להיות מורכב מסכום של איברים בודדים (אפס, הרמוניות בסיסיות וגבוהות יותר):

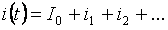
ניתן לקבוע את ערך ה-rms של זרם הענף הכולל על ידי הערך הממוצע של הזרמים ההרמוניים הבודדים:

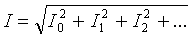
ההספק הפעיל של הזרם הלא-סינוסואידי שווה לסכום ההספקים הפעילים של ההרמוניות האישיות:

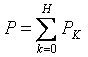
להלן דוגמה כללית לחישוב מעגלי זרם לא-סינוסואידיים. לכל הזרמים, המתחים, ההתנגדויות יהיו שני מדדים: הספרה הראשונה פירושה מספר הענף והספרה השנייה - המספר ההרמוני. מתח נכנס:

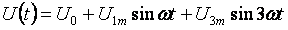
• מרכיב קבוע

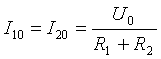
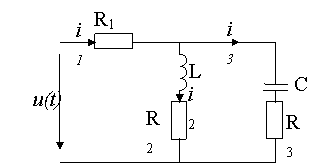
איור 2. תרשים חשמלי

• הרמונית מרכזית:

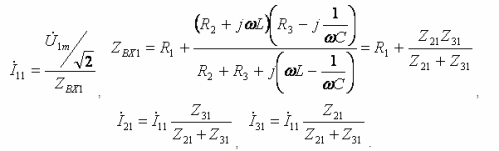
• הרמוניה שלישית:

קרא גם: תוכניות תיקון AC ל DC הנפוצות ביותר