תנודות מתמשכות ותהודה פרמטרית
תנודות מתמשכות - תנודות שהאנרגיה שלהן לא משתנה עם הזמן. במערכות פיזיקליות אמיתיות, תמיד יש סיבות הגורמות למעבר של אנרגיית רטט לאנרגיה תרמית (למשל חיכוך במערכות מכניות, התנגדות אקטיבית במערכות חשמליות).
לכן, ניתן להשיג תנודות ללא דכדוך רק בתנאי שהפסדי האנרגיה הללו יתחדשו. חידוש כזה מתרחש באופן אוטומטי במערכות נדנודות עצמיות עקב אנרגיה ממקור חיצוני. תנודות אלקטרומגנטיות מתמשכות נמצאות בשימוש נרחב ביותר. כדי להשיג אותם משתמשים בגנרטורים שונים.

כדי להפוך רעידות חשמליות או מכניות (של מעגל נדנוד או מטוטלת) ללא דכדוך, יש צורך לפצות על התנגדות או הפסדי חיכוך בכל עת.
לדוגמה, אתה יכול לפעול על המעגל המתנודד עם EMF לסירוגין, אשר יגדיל מעת לעת את הזרם בסליל ובהתאם, ישמור על משרעת המתח בקבל.או שאתה יכול לדחוף את המטוטלת בצורה דומה, ולהשאיר אותה מתנדנדת בהרמוניה.
כפי שאתה יודע, גודל האנרגיה של השדה המגנטי של סליל המעגל המתנודד קשור להשראות ולזרם שלו על ידי הקשר הבא (הנוסחה השנייה היאאנרגיה של השדה החשמלי של הקבל אותו קו מתאר)
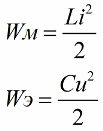
ברור מהנוסחה הראשונה שאם נגדיל מעת לעת את הזרם בסליל, הפועל על מעגל ה-EMF המתחלף, אז (על ידי הגדלת או הקטנה של הגורם השני בנוסחה - זרם) נחדש מעת לעת את המעגל הזה באנרגיה.
פעולה על המעגל אך ורק בזמן עם התנודות החופשיות הטבעיות שלו, כלומר בתדר התהודה, נקבל את התופעה של תהודה חשמלית, מכיוון שהיא בתדר התהודה מערכת מתנודדת סופג בצורה האינטנסיבית ביותר את האנרגיה המסופקת לו.
אבל מה אם אתה משנה מעת לעת לא את הגורם השני (לא זרם או מתח), אלא את הגורם הראשון - השראות או קיבול? במקרה זה, המעגל יעבור גם שינוי באנרגיה שלו.
לדוגמה, מעת לעת דחיפה של הליבה פנימה והחוצה מהסליל או דחיפה פנימה והחוצה מהקבלדיאלקטרי, - אנו מקבלים גם שינוי תקופתי מאוד ברור באנרגיה במעגל.
אנו כותבים את המיקום הזה עבור שינוי יחידה בשראות הסליל:
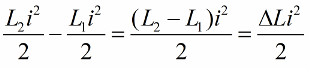
ההשפעה הבולטת ביותר של תנופת המעגל תהיה אם שינויי השראות יבוצעו בדיוק בזמן. לדוגמה, אם ניקח את אותו מעגל בכל רגע בזמן, כאשר זרם i כבר זורם דרכו, ונכניס ליבה לתוך הסליל, אז האנרגיה תשתנה בכמות הבאה:
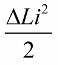
עכשיו תן לתנודות חופשיות להופיע במעגל עצמו, אבל ברגע שבו, לאחר רבע תקופה, האנרגיה עברה לחלוטין לתוך הקבל והזרם בסליל הפך לאפס, נוציא בפתאומיות את הליבה מהסליל השראות יחזור למצבו המקורי, לערך ההתחלתי L. אין צורך להשקיע עבודה כנגד השדה המגנטי בעת הסרת הליבה. לכן, כאשר הליבה נדחפה לתוך הסליל, המעגל קיבל אנרגיה, מאז שעבדנו, שערכה:
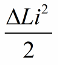
לאחר רבע מהתקופה הקבל מתחיל להיפרק, האנרגיה שלו מומרת שוב לאנרגיית השדה המגנטי של הסליל, כאשר השדה המגנטי יגיע למשרעת, נלחץ שוב בחדות על הליבה. שוב השראות גדלה, גדלה באותה כמות.
ושוב, בזרם אפס, אנו מחזירים את השראות לערכה המקורי. כתוצאה מכך, אם רווחי האנרגיה עבור כל חצי מחזור עולים על הפסדי ההתנגדות, האנרגיה של הלולאה תגדל כל הזמן ומשרעת התנודה תגדל. מצב זה מתבטא באי השוויון:
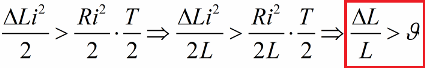
כאן חילקנו את שני הצדדים של אי השוויון הזה ב-L ורשמנו את התנאי לאפשרות של עירור פרמטרי על ידי קפיצות עבור ערך מסוים של הירידה הלוגריתמית.
מומלץ לשנות את השראות (או הקיבול) פעמיים בכל תקופה, לכן תדירות שינוי הפרמטר (תדר תהודה פרמטרי) צריכה להיות כפולה מהתדר הטבעי של המערכת המתנודדת:
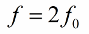
אז נתיב העירור של תנודות במעגל הופיע ללא צורך בשינוי ישיר של EMF או הזרם.הזרם התנודות הראשוני במעגל קיים תמיד בצורה כזו או אחרת, וזה אפילו לא לוקח בחשבון הפרעות מתנודות בתדרי רדיו באטמוספירה.
אם השראות (או הקיבול) לא משתנה בקפיצות, אלא בצורה הרמונית, אז התנאי להתרחשות תנודות ייראה קצת אחרת:
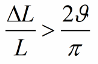
מכיוון שקיבול והשראות הם פרמטרים של מעגל (כגון מסה של מטוטלת או גמישות של קפיץ), שיטת התנודות המלהיבה נקראת גם עירור פרמטרי.
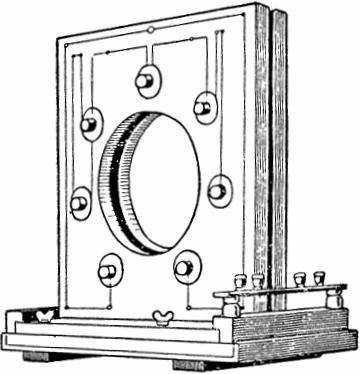
תופעה זו התגלתה ונחקרה באופן מעשי בתחילת המאה ה-20 על ידי הפיזיקאים הסובייטים מנדלשטם ופפאלקסי. בהתבסס על תופעה פיזיקלית זו, הם בנו את מחולל AC פרמטרי ראשון עם הספק של 4 קילוואט והשראות משתנה.
בתכנון הגנרטור מוקמו משני צידי המסגרת שבעה זוגות של סלילים שטוחים, שבחללם הסתובב דיסק פרומגנטי עם בליטות. כאשר הדיסק מונע להסתובב על ידי מנוע, הבליטות שלו נעות מעת לעת פנימה והחוצה מהרווח שבין כל זוג סלילים, ובכך משנים את השראות והתנודות המרגשות.
