מהו אספקת חשמל?

האדם המודרני נתקל כל הזמן בחשמל בחיי היומיום ובעבודה, משתמש במכשירים הצורכים זרם חשמלי ובמכשירים המייצרים אותו. כשאתה עובד איתם, אתה תמיד צריך לקחת בחשבון את היכולות שלהם הגלומות במאפיינים הטכניים.

אחד המדדים העיקריים של כל מכשיר חשמלי הוא כמות פיזית כמו אנרגיה חשמלית... נהוג לקרוא לעוצמת או מהירות היצירה, ההולכה או ההמרה של חשמל לסוגי אנרגיה אחרים, למשל, חום, אור, מֵכָנִי.

הובלה או העברה של אנרגיה חשמלית גדולה למטרות תעשייתיות מתבצעת על פי קווי מתח גבוה.

טרנספורמציה אנרגיה חשמלית מתבצע בתחנות משנה שנאים.

צריכת החשמל מתרחשת במכשירים ביתיים ותעשייתיים למטרות שונות. אחד הסוגים הנפוצים שלהם הם מנורות ליבון בדירוגים שונים.

להספק החשמלי של גנרטורים, קווי מתח וצרכנים במעגלי DC ו-AC יש אותה משמעות פיזיקלית, המתבטאת בו-זמנית ביחסים שונים בהתאם לצורת האותות המרוכבים. כדי להגדיר את הדפוסים הכלליים, מושגים של ערכים מיידיים... הם שוב מדגישים את התלות של קצב הטרנספורמציה של חשמל בזמן.

קביעת הספק חשמלי מיידי

בהנדסת חשמל תיאורטית, על מנת לגזור את היחסים הבסיסיים בין זרם, מתח והספק, משתמשים בתמונות שלהם בצורה של ערכים מיידיים, המקובעים בנקודת זמן מסוימת.

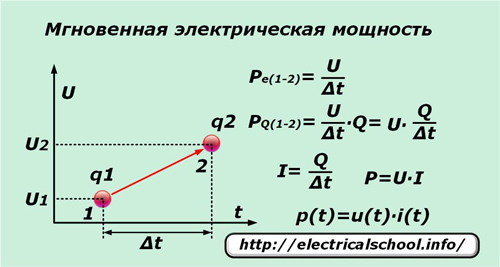
אם תוך פרק זמן קצר מאוד ∆t מטען אלמנטרי יחיד q בהשפעת המתח U עובר מנקודה «1» לנקודה «2», אז הוא מבצע עבודה השווה להפרש הפוטנציאל בין הנקודות הללו. לחלק אותו במרווח הזמן ∆t, נקבל את הביטוי להספק המיידי ליחידת מטען Pe (1-2).

מכיוון שלא רק המטען הבודד נע תחת פעולת המתח המופעל, אלא גם כל הסמוכים שנמצאים תחת השפעת הכוח הזה, שמספרם מיוצג בנוחות על ידי המספר Q, אז הערך המיידי של ההספק PQ (1-2) ניתן לכתוב עבורם.

לאחר ביצוע טרנספורמציות פשוטות, נקבל את הביטוי להספק P ואת התלות של הערך המיידי שלו p (t) במרכיבי המכפלה של הזרם המיידי i (t) והמתח u (t).

קביעת הספק חשמלי קבוע

V מעגלי DC גודל מפל המתח בקטע המעגל והזרם הזורם דרכו אינו משתנה ונשאר יציב, שווה לערכים המיידיים.לכן, ההספק במעגל זה יכול להיקבע על ידי הכפלת ערכים אלה או חלוקת העבודה המושלמת A בתקופת ביצועה, כפי שמוצג בתמונת ההסבר.

קביעת הספק החשמלי של זרם חילופין

חוקי הווריאציה הסינוסואידלית של זרמים ומתחים המועברים דרך רשתות חשמליות כופים את השפעתם על ביטוי הכוח במעגלים כאלה. כאן נכנס לתמונה כוח לכאורה, המתואר על ידי משולש הכוח ומורכב ממרכיבים פעילים ותגובתיים.

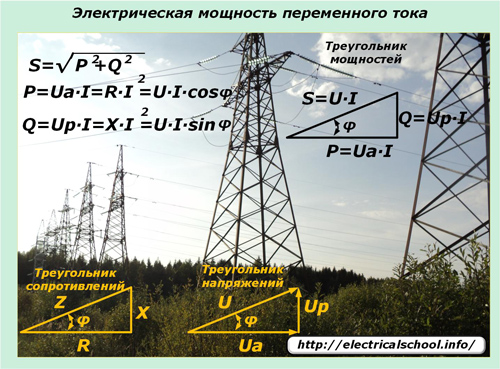
זרם חשמלי סינוסואידי כאשר עובר דרך קווי מתח עם סוגי עומסים מעורבים בכל המקטעים אינו משנה את צורת ההרמוניה שלו.ונפילת המתח בעומסים תגובתיים עוברת פאזה בכיוון מסוים. ביטויי ערכי רגע עוזרים להבין את השפעת העומסים המופעלים על שינוי ההספק במעגל וכיוונו.

יחד עם זאת, שימו לב מיד לעובדה שכיוון זרימת הזרם מהגנרטור לצרכן וההספק המועבר דרך המעגל שנוצר הם דברים שונים לחלוטין, שבמקרים מסוימים עשויים לא רק שלא לחפף, אלא גם להיות. מכוון לכיוונים מנוגדים.

שקול את היחסים הללו בביטוי האידיאלי והטהור שלהם עבור סוגים שונים של עומסים:

• פָּעִיל;

• קיבולי;

• אִינְדוּקְטִיבִי.

פיזור כוח עומס אקטיבי

נניח שהגנרטור מייצר מתח סינוסואידי אידיאלי u המופעל על ההתנגדות הפעילה בלבד של המעגל. מד זרם A ומד מתח V מודדים זרם I ומתח U בכל פעם t.

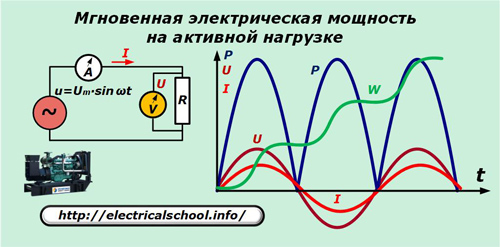
הגרף מראה שהסינוסואידים של הזרם וירידת המתח על פני ההתנגדות הפעילה תואמים בתדירות ובפאזה, מה שיוצר את אותן תנודות. הכוח המובע על ידי התוצר שלהם מתנודד בתדירות כפולה ונשאר תמיד חיובי.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

אם נלך לביטוי מתח הפעלה, אז נקבל: p = P ∙ (1-cos2ωt).

לאחר מכן נשלב את ההספק לאורך התקופה של תנודה אחת T ונוכל להבחין שרווח האנרגיה ∆W במהלך המרווח הזה גדל. עם הזמן, ההתנגדות ממשיכה לצרוך חלקים חדשים של חשמל, כפי שמוצג בגרף.

עם עומסים תגובתיים, המאפיינים של צריכת האנרגיה שונים, יש להם צורה שונה.

פיזור כוח קיבולי

במעגל החשמלי של הגנרטור, החלף את האלמנט ההתנגדות בקבל עם קיבול C.

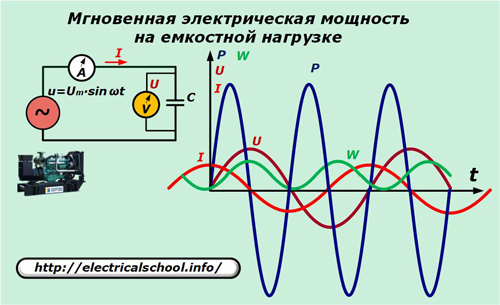
הקשר בין הזרם לירידת המתח בקיבול מתבטא ביחס: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

אנו מכפילים את ערכי הביטויים המיידיים של הזרם עם המתח ומקבלים את ערך ההספק שנצרך על ידי העומס הקיבולי.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt sin = U2/ (2X.

כאן אתה יכול לראות שההספק נע סביב האפס בתדירות כפולה מהמתח המופעל. הערך הכולל שלו לתקופה ההרמונית, כמו גם רווח האנרגיה, הוא אפס.

משמעות הדבר היא שאנרגיה נעה לאורך המעגל הסגור של המעגל בשני הכיוונים, אך אינה פועלת.עובדה כזו מוסברת על ידי העובדה שכאשר מתח המקור עולה בערך המוחלט, ההספק חיובי, וזרימת האנרגיה דרך המעגל מופנית למיכל, שם נצברת אנרגיה.

לאחר שהמתח עובר לקטע ההרמוני הנופל, אנרגיה מוחזרת מהקבל למעגל אל המקור. לא נעשית עבודה מועילה באף אחד מהתהליכים.

פיזור הספק בעומס אינדוקטיבי

כעת, במעגל האספקה, החלף את הקבל בשראות L.

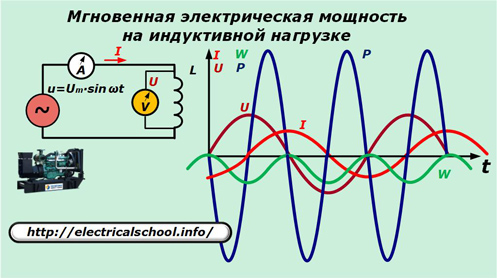
כאן הזרם דרך השראות מבוטא על ידי היחס:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

ואז אנחנו מקבלים

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙L sinω2ωt ∙.

הביטויים המתקבלים מאפשרים לנו לראות את אופי השינוי בכיוון הכוח ועליית האנרגיה על השראות, אשר מבצעים את אותן תנודות שאינן שימושיות לביצוע עבודה, כמו בקיבול.

הכוח המשתחרר בעומסים תגובתיים נקרא רכיב תגובתי. בתנאים אידיאליים, כאשר לחוטי החיבור אין התנגדות אקטיבית, הוא נראה בלתי מזיק ואינו גורם נזק. אבל בתנאי הספק אמיתיים, ארעיות תקופתיות ותנודות הספק תגובתי גורמים לחימום של כל האלמנטים הפעילים, כולל חוטי חיבור, שעבורם נצרך אנרגיה מסוימת וערך הכוח המלא המופעל של המקור יורד.

ההבדל העיקרי בין הרכיב התגובתי של הכוח הוא שהוא אינו מבצע עבודה שימושית כלל, אלא מוביל לאובדן אנרגיה חשמלית ועומסים עודפים על ציוד, אשר מסוכנים במיוחד במצבים קריטיים.

מסיבות אלה, כדי לבטל את השפעת הכוח התגובתי, בפרט מערכות טכניות לתמורה.

חלוקת כוח בעומס מעורב

כדוגמה, אנו משתמשים בעומס של גנרטור עם מאפיין קיבולי פעיל.

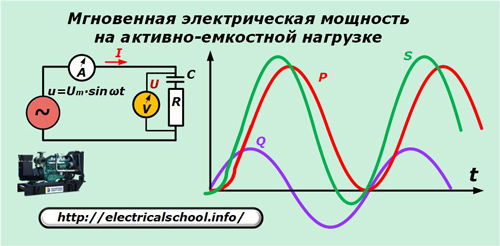
כדי לפשט את התמונה, הסינוסואידים של זרמים ומתחים אינם מוצגים בגרף הנתון, אך יש לזכור כי עם אופי פעיל-קיבולי של העומס, וקטור הזרם מוביל את המתח.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

לאחר טרנספורמציות נקבל: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

שני המונחים הללו בביטוי האחרון הם המרכיבים הפעילים והתגובתיים של הכוח הנראה המיידי. רק הראשון שבהם עושה עבודה מועילה.

כלי מדידת כוח

כדי לנתח את צריכת החשמל ולחשב עבורה, משתמשים במכשירי מדידה, שנקראו זה מכבר "מונים"… עבודתם מבוססת על מדידת הערכים האפקטיביים של זרם ומתח והכפלה אוטומטית שלהם עם פלט של מידע.

מונים מציגים את צריכת האנרגיה על ידי ספירת זמן ההפעלה של מכשירי חשמל על בסיס אינקרמנטלי מרגע הפעלת המונה בעומס.

כדי למדוד את הרכיב הפעיל של הספק במעגלי AC, מדי וואט, ותגובתי - מחממים. יש להם ייעודי יחידות שונים:

• וואט (W, W);

• var (var, var, var).

כדי לקבוע את צריכת האנרגיה הכוללת, יש צורך לחשב את ערכה באמצעות נוסחת משולש הכוח המבוססת על קריאות מד הוואטים וה-varmeter. זה מתבטא ביחידות משלו - וולט-אמפר.

הייעודים המקובלים של היחידות של כל אחד מסייעים לחשמלאים לשפוט לא רק את ערכו, אלא גם את אופי מרכיב הכוח.