תהודה של זרמים

חיבור מקביל של קבל ומשרן במעגל זרם חילופין

קחו בחשבון את התופעות בשרשרת זרם חליפיןמכיל גנרטור, קבל ומשרן המחוברים במקביל. נניח שלמעגל אין התנגדות אקטיבית.

ברור שבמעגל כזה המתח של הסליל וגם של הקבל בכל עת שווה למתח שפותח על ידי הגנרטור.

הזרם הכולל במעגל מורכב מהזרמים בענפים שלו. הזרם בענף האינדוקטיבי מפגר את המתח בפאזה ברבע מהתקופה, והזרם בענף הקיבולי מוביל אותו באותו רבע של התקופה. לכן, הזרמים בענפים בכל רגע של זמן מתבררים כמוסטים פאזה ביחס זה לזה בחצי תקופה, כלומר, הם נמצאים באנטי-פאזה. לפיכך, הזרמים בענפים בכל עת מופנים זה לזה, והזרם הכולל בחלק הלא מסועף של המעגל שווה להפרש שלהם.

זה נותן לנו את הזכות לכתוב שוויון I = IL -מעגל אינטגרלי

איפה אני- ערך אפקטיבי של הזרם הכולל במעגל, I L ומעגל משולב - ערכים יעילים של זרמים בענפים.

באמצעות חוק אוהם כדי לקבוע את הערכים האפקטיביים של הזרם בענפים, אנו מקבלים:

Il = U / XL ו- Az° C = U / XC

אם המעגל נשלט על ידי התנגדות אינדוקטיבית, כלומר. XL יותר ▼ XC, הזרם בסליל קטן מהזרם בקבל; לכן הזרם בקטע הלא מסועף של המעגל הוא קיבולי בטבעו והמעגל בכללותו עבור הגנרטור יהיה קיבולי. לעומת זאת, כאשר XC גדול מ-XL, הזרם בקבל קטן מהזרם בסליל; לכן הזרם בקטע הלא מסועף של המעגל הוא אינדוקטיבי, והמעגל בכללותו של הגנרטור יהיה אינדוקטיבי.

אין לשכוח שבשני המקרים העומס הוא תגובתי, כלומר. המעגל אינו צורך את הכוח של הגנרטור.

תהודה של זרמים

הבה נבחן כעת את המקרה כאשר הקבל והסליל המחוברים במקביל התבררו כשווים בתגובתם, כלומר. XlL = X°C.

אם, כמו קודם, נניח שלסליל ולקבל אין התנגדות אקטיבית, אז אם התגובות שלהם שוות (YL = Y° C) הזרם הכולל בחלק הלא מסועף של המעגל יהיה אפס, בעוד שבענפים שווה זרמים יזרמו בעוצמה הגדולה ביותר. במקרה זה, התופעה של זרמי תהודה מתרחשת במעגל.

בתהודה זרם, הערכים האפקטיביים של הזרמים בכל ענף, הנקבעים על ידי היחסים IL = U / XL ו- Аz° С = U / XC יהיו שווים זה לזה, כך ש-XL = XC.

המסקנה שהגענו אליה עשויה להיראות די מוזרה במבט ראשון. למעשה, הגנרטור טעון בשתי התנגדויות ואין זרם בחלק הבלתי מסועף של המעגל, בעוד שזרמים שווים, ויותר מכך, זורמים בהתנגדויות עצמן.

זה מוסבר על ידי התנהגות השדה המגנטי של הסליל ו שדה חשמלי של קבל... בהדהוד של זרמים, כמו ב תהודה של מתח, ישנה תנודת אנרגיה בין שדה הסליל לשדה הקבל. הגנרטור, לאחר העברת האנרגיה למעגל, נראה מבודד. ניתן לכבות אותו לחלוטין והזרם בחלק המסועף של המעגל יישמר ללא גנרטור על ידי האנרגיה שהמעגל אוגר בתחילה. כמו כן, המתח על פני מסופי המעגל יישאר בדיוק זהה לזה שפותח על ידי הגנרטור.

כך, כשהמשרן והקבל מחוברים במקביל, קיבלנו מעגל מתנד השונה מזה שתואר לעיל רק בכך שהגנרטור שיוצר את התנודות אינו מחובר ישירות למעגל והמעגל סגור. 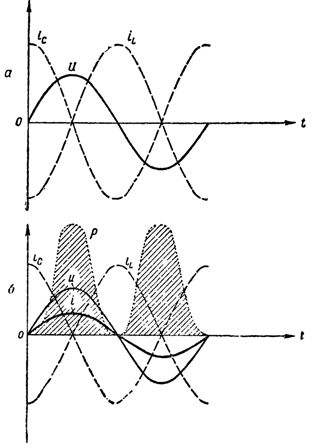גרפים של זרמים, מתח והספק במעגל בתהודה של זרמים: א - ההתנגדות הפעילה שווה לאפס, המעגל אינו צורך אנרגיה; ב - למעגל יש התנגדות פעילה, זרם הופיע בחלק הלא מסועף של המעגל, המעגל צורך אנרגיה

L, C ו-e, שבהן מתרחשת תהודה זרם, נקבעים, כמו בתהודה של מתח (אם אנו מזניחים את ההתנגדות הפעילה של המעגל), על ידי השוויון:

ωL = 1 / ω° C

לָכֵן:

eres = 1 / 2π√LC

Lres = 1 / ω2C

חתיכה = 1 / ω2L

על ידי שינוי כל אחת משלושת הכמויות הללו, ניתן להשיג את השוויון Xl = X° C, כלומר להפוך את המעגל למעגל מתנודד.

אז, יש לנו מעגל נדנוד סגור שבו אנו יכולים לגרום לתנודות חשמליות, כלומר. זרם חליפין. ואלמלא ההתנגדות הפעילה שיש לכל מעגל מתנודד, זרם חילופין עלול להתקיים בו ללא הרף.הנוכחות של התנגדות אקטיבית מובילה לכך שהתנודות במעגל מתפוגגות בהדרגה, וכדי לשמור עליהן יש צורך במקור אנרגיה - אלטרנטור.

במעגלי זרם שאינם סינוסואידים, מצבי תהודה אפשריים עבור רכיבים הרמוניים שונים.

זרמים תהודה נמצאים בשימוש נרחב בפועל. תופעת תהודה זרם משמשת במסנני פס פס כ"מהדק" חשמלי המעכב תדר מסוים. מכיוון שקיימת התנגדות זרם משמעותית בתדר f, ירידת המתח במעגל בתדר f תהיה מקסימלית. תכונה זו של הלולאה נקראת סלקטיביות, היא משמשת במקלטי רדיו כדי לבודד את האות של תחנת רדיו מסוימת. מעגל נדנוד הפועל במצב תהודה של זרמים הוא אחד המרכיבים העיקריים גנרטורים אלקטרוניים.