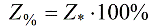מערכת של יחידות יחסיות
כדי לפשט את החישובים בעת חישוב פרמטרים במערכות הולכת כוח, נעשה שימוש במערכת של יחידות יחסיות. שיטה זו כוללת ביטוי של הערך הנוכחי של ערך המערכת במונחים של ערך הבסיס (הבסיס) שנלקח כיחידה.
אז הערך היחסי מבוטא כמכפיל של ערך הבסיס (זרם, מתח, התנגדות, הספק וכו') ואינו תלוי, מבוטא ביחידות יחסיות, ברמת המתח. בספרות האנגלית, יחידות יחסיות מסומנות pu או p.u. (ממערכת של יחידה - מערכת של יחידות יחסיות).
לדוגמה, עבור שנאים מאותו סוג, נפילת מתח, עכבה והפסדים שונים בערכם המוחלט במתחים מיושמים שונים. אבל בגדלים יחסיים הם יישארו בערך אותו הדבר. לאחר ביצוע החישוב, התוצאות מומרות בקלות חזרה ליחידות מערכת (באמפר, בוולט, באוהם, בוואט וכו') מכיוון שערכי הבסיס שאליהם משווים את ערכי הזרם ידועים בתחילה.
ככלל, יחידות יחסיות נוחות לחישוב הספק משודר, אך לעתים קרובות קורה שהפרמטרים של גנרטורים ושנאים מנוע מוגדרים ביחידות יחסיות, כך שכל מהנדס צריך להכיר את המושג יחידות יחסיות. יחידות ההספק, הזרם, המתח, העכבה והכניסה משמשות במערכת היחידה היחסית. כוח ומתח הם כמויות בלתי תלויות, המוכתבות על ידי התכונות של מערכות אנרגיה אמיתיות.
ניתן לבטא את כל ערכי הרשת של המערכת ככפולות של ערכי בסיס נבחרים. אז אם אנחנו מדברים על כוח, אז את ההספק המדורג של השנאי ניתן לבחור כערך הבסיס. קורה שהכוח המתקבל ברגע מסוים בצורה של ערך יחסי מקל מאוד על חישובים. הבסיס למתח הוא מתח האוטובוס הנומינלי וכו'.
באופן כללי, ההקשר תמיד מאפשר לך להבין באיזה ערך יחסי מדובר, ואפילו נוכחותו של אותו סמל "פו" בספרות האנגלית לא תבלבל אותך.
אז כל הכמויות הפיזיקליות של המערכת נקראות. אבל כאשר אנו מתרגמים אותם ליחידות יחסיות (למעשה לאחוזים), אופי החישובים התיאורטיים מוכלל.
הערך היחסי של כמות פיזיקלית כלשהי מובן כקשר שלה עם ערך בסיס כלשהו, כלומר עם הערך שנבחר כיחידה למדידה נתונה. הערך היחסי מסומן בכוכבית למטה.
לעתים קרובות, הערכים הבסיסיים הבאים נלקחים בחישובים: התנגדות בסיסית, זרם בסיסי, מתח בסיסי והספק בסיסי.
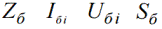
הכיתוב "b" מציין שזהו ערך בסיס.
ואז יחידות המדידה היחסיות ייקראו בסיסיות יחסית:
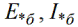
הכוכבית מציינת את הערך היחסי, האות «b» - הבסיס. EMF הוא בסיסי יחסית, הנוכחי הוא בסיסי יחסית וכו'. ויחידות הבסיס היחסיות ייקבעו על ידי הביטויים הבאים:
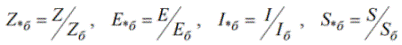
לדוגמה, כדי למדוד מהירויות זוויתיות, המהירות הסינכרונית הזוויתית נלקחת כאחדות ולכן המהירות הזוויתית הסינכרונית תהיה שווה למהירות הזוויתית הבסיסית.
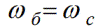
אז ניתן לבטא מהירות זוויתית שרירותית ביחידות יחסיות:
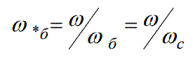
בהתאם, ניתן לקחת את היחסים הבאים כבסיסיים עבור הצמדת שטף ועבור השראות:
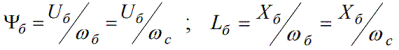
כאן, הצמדת השטף העיקרית היא הצמדת השטף שגורמת למתח העיקרי במהירות הזוויתית העיקרית.
אז אם לוקחים את המהירות הזוויתית הסינכרונית כבסיס, אז:
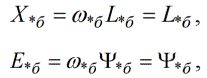
ביחידות יחסיות, emf שווה לשטף והתנגדות אינדוקטיבית שווה לשראות. הסיבה לכך היא שיחידות הבסיס נבחרות כראוי.
לאחר מכן שקול את מתח הפאזה ביחידות יחסיות ובסיסיות:
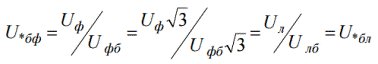
קל לראות שמתח הפאזה ביחידות יסוד יחסיות מתברר כשווה למתח היסודי היחסי הליניארי. באופן דומה, הערך של משרעת המתח ביחידות יחסיות מתברר כשווה לאפקטיבי:
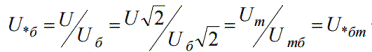
מתלות אלו ניכר כי ביחידות יחסיות אפילו הספק של שלוש פאזות והספק של שלב אחד שווים, וגם זרמי העירור, השטפים וה-emf של המחולל - מתגלים כשווים זה לזה.
חשוב לציין כאן שלכל אלמנט במעגל, ההתנגדות היחסית תהיה שווה למפל המתח היחסי בתנאי ההספק המדורג המסופק למעגל.
בעת חישוב זרמי קצר חשמלי, משתמשים בארבעה פרמטרים עיקריים: זרם, מתח, התנגדות והספק. ערכי היסוד של מתח והספק נתפסים כעצמאיים, ובאמצעותם באים לידי ביטוי ההתנגדות והזרם הבסיסיים. מתוך משוואת ההספק של רשת תלת פאזית - זרם, אם כן חוק אוהם - התנגדות:
מכיוון שניתן לבחור את ערך הבסיס באופן שרירותי, לאותה כמות פיזיקלית יכולה להיות ערכים מספריים שונים, המבוטאת ביחידות יחסיות. לכן, ההתנגדויות היחסיות של גנרטורים, מנועים, שנאים נקבעות ביחידות יחסיות על ידי הזנת יחידות נומינליות יחסיות. Sn - כוח נומינלי. Un - מתח נומינלי. ערכים נומינליים יחסיים נכתבים עם אינדקס «n»:
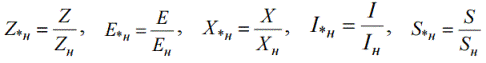
כדי למצוא את ההתנגדויות והזרמים הנומינליים, נעשה שימוש בנוסחאות הסטנדרטיות:
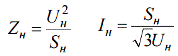
כדי לבסס את הקשר בין יחידות יחסיות וכמויות בשמות, תחילה מבטאים את הקשר בין הבסיס היחסי לכמויות הבסיס:
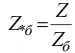
בואו נכתוב את ההתנגדות הבסיסית במונחים של כוח ותחליף:
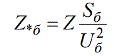
אז אתה יכול לתרגם את הערך שצוין לערך בסיס יחסי.
ובאופן דומה אתה יכול לבסס קשר בין יחידות נומינליות יחסיות ושמות עצם:
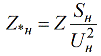
כדי לחשב את ההתנגדות ביחידות עם שם עם ערכים נומינליים יחסיים ידועים, השתמש בנוסחה הבאה:
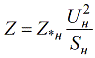
הקשר בין יחידות נומינליות יחסיות ליחידות בסיס יחסיות נקבע על ידי הנוסחה הבאה:
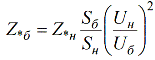
באמצעות נוסחה זו, ניתן להמיר יחידות נומינליות יחסיות ליחידות בסיס יחסיות.
במערכות חשמל, כדי להגביל זרמי קצר חשמלי, הגדר כורים מוגבלים כיום, למעשה - משרנים ליניאריים. הם מקבלים מתח וזרם מדורג אבל לא כוח.
בהתחשב בכך ש
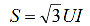
והפיכת הביטויים לעיל עבור התנגדות הבסיס הנומינלית והיחסית היחסית, נקבל:
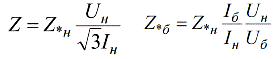
ניתן לבטא ערכים יחסיים באחוזים:
