טופולוגיות מעגלים - מושגי יסוד

מעגל חשמלי הוא קבוצה של מכשירים (אלמנטים) וחוטי החיבור שלהם שדרכם יכול לזרום זרם חשמלי. כל האלמנטים של מעגלים חשמליים חולקים בפאסיבי ובאקטיבי.

יסודות פעילים ממירים סוגים שונים של אנרגיה (מכנית, כימית, אור וכו') לאנרגיה חשמלית. במכשירים פסיביים, אנרגיה חשמלית מומרת לסוגים אחרים של אנרגיה. אלמנטים פעילים נקראים מקורות, פסיביים נקראים צרכנים או מקלטים.

בתורת המעגלים, מודלים אידיאלים של אלמנטים חשמליים נחשבים. זה הופך את תיאור האלמנטים לפשוט ככל האפשר. אלמנטים אמיתיים מורכבים יותר מעוצבים מתוך קבוצה של אלמנטים אידיאלים.

האלמנטים הפסיביים העיקריים של מעגלים חשמליים הם נגד (אלמנט התנגדות), משרן (אלמנט אינדוקטיבי) וקבלים (אלמנט קיבולי). אלמנטים מותקנים במעגל חשמלי כדי ליצור מתח וזרם בעלי ערך וצורה נתונים (ראה - מעגל חשמלי ומרכיביו).

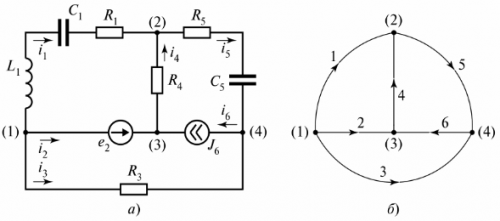
מעגל חשמלי מורכב מענפים וצמתים. ענף - זהו קטע של מעגל חשמלי (מעגל) שדרכו זורם אותו זרם. קשר - חיבור של שלושה סניפים או יותר. בתרשים החשמלי, הצומת מסומן על ידי נקודה (איור 1).

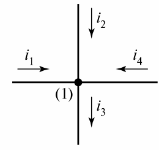
אורז. 1. הגדר את הצומת בתרשים

במידת הצורך, הצמתים של הדיאגרמה ממוספרים משמאל לימין מלמעלה למטה.

באיור. 2 מציג את הענף ההתנגדות-קיבולי שבו זורם ה-iC הנוכחי.

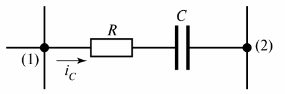
אורז. 2. ענף התנגדות-קיבולי

ניתן לתת הגדרה נוספת של ענף - זהו קטע של מעגל בין שני צמתים סמוכים (צמתים (1) ו- (2) באיור 2).

שַׁרשֶׁרֶת האם יש נתיב סגור כלשהו במעגל החשמלי. ניתן לסגור את המעגל על ​​ידי כל ענף, כולל ענפים מותנים שהתנגדותם שווה לאינסוף.

באיור. 3 מציג מעגל חשמלי מסועף המורכב משלושה ענפים.

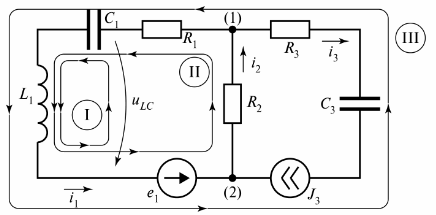
אורז. 3. מעגל חשמלי עם שני מעגלים

התרשים מציג שלושה מעגלים, ומעגל I נסגר על ידי ענף של התנגדות אינסופית. ענף זה מסומן כמתח tiLC.

עבור המעגל של איור. 3 אפשר להרכיב לולאות רבות הסגורות על ידי ענפים אמיתיים או מותנים, אך לחישוב רעש חשמלי נעשה שימוש במושג "לולאה עצמאית". מספר לולאות המעגל העצמאיות מוגדר תמיד כמינימום הנדרש לחישוב.

מעגלים עצמאיים תמיד סגורים, אך ענפים בעלי התנגדות שאינה שווה לאינסוף, וכל מעגל עצמאי כולל לפחות ענף אחד שאינו כלול במעגלים אחרים. עבור מעגלים חשמליים מורכבים, אתה יכול לקבוע את מספר המעגלים העצמאיים באמצעות דיאגרמת המעגלים.

על דיאגרמת המעגל ייצוג מותנה של המעגל נקרא, שבו כל ענף מוחלף בקטע קו. פריטים בסניפים אינם מוצגים. לדוגמה, באיור. 4 מציג מעגל ענף ותרשים שלו.

אורז. 4. מעגל חשמלי מסועף: א - דיאגרמת מעגל, ב - דיאגרמה

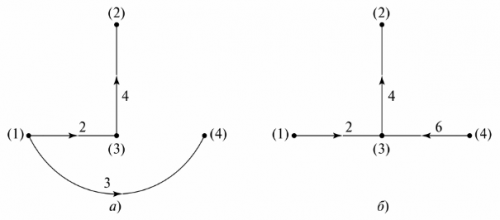
כדי ליצור דיאגרמה של דיאגרמה, עליך לחבר את הצמתים עם קווי הסתעפות מבלי לציין אלמנטים עליהם. הענפים ממוספרים, וכיווני הזרמים עליהם מסומנים בחצים. לגרף עצמו אין משמעות פיזיקלית, אך ניתן להשתמש בו כדי לקבוע את מספר וסוג קווי המתאר העצמאיים. לשם כך מכינים "עץ גרפי".

עץ גרפי הוא מייצג את הגרף של מעגל שהצמתים שלו מחוברים על ידי ענפים בצורה כזו שלא נוצרת לולאה סגורה. עשויות להיות מספר אפשרויות להצגת עץ גרפי. באיור. 5 מציג שתי אפשרויות אפשריות עבור המעגל של איור. 4.

אורז. 5. עץ גרפי של התוכנית

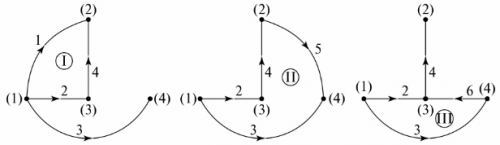
מספר הענפים החסרים בעץ הגרף שווה למספר הלולאות העצמאיות של המעגל. בדוגמה, אלו שלושה ענפים, שלוש לולאות עצמאיות. ניתן לקבל את התצורה של לולאות עצמאיות על ידי חיבור רציף של הצמתים של עץ הגרף עם ענפים שאינם מצוינים בעץ הגרף. לדוגמה, עבור עץ הגרפים באיור. 5, וקווי המתאר העצמאיים מוצגים באיור. 6.

אורז. 6. קביעת קווי מתאר עצמאיים דרך עץ הגרפים

בחירת אפשרות להגדיר מעגלים עצמאיים לחישוב המעגל מתבצעת במהלך ניתוח מעגלים. כדאי לבחור קווי מתאר כאלה כדי שהחישוב יהיה פשוט ככל האפשר, כלומר. מספר המשוואות התלויות במערכת הוא מינימלי.

משוואות טופולוגיות קובעות קשר בין מתחים וזרמים במעגל, ומספר וסוג המשוואות אינם תלויים באילו אלמנטים נכללים בענפים. משוואות טופולוגיות כוללות משוואות המורכבות מהן לפי חוקי קירכהוף.