אלקטרונים מתנהגים כמו גלים

פיזיקאים יודעים מזמן שאור הוא גל אלקטרומגנטי. עד היום אף אחד לא מטיל ספק בעמדה זו, שכן האור מדגים בבירור את כל הסימנים של התנהגות גל: גלי אור יכולים לחפוף זה את זה, ליצור דפוס הפרעה, הם גם מסוגלים להיפרד, להתכופף סביב מכשולים לאורך זמן העקיפה.

כאשר אנו רואים ציפור שהולכת כמו ברווז, שוחה כמו ברווז ומנקרת כמו ברווז, אנו קוראים לציפור הזו ברווז. אז האור הוא גל אלקטרומגנטימבוסס על סימנים שנצפו באופן אובייקטיבי להתנהגות של גל כזה באור.

עם זאת, בסוף המאה ה-19 וה-20, פיזיקאים היו אמורים להתחיל לדבר על "דואליזם גל החלקיקים" של האור. מסתבר שהידיעה שאור הוא גל אלקטרומגנטי היא לא כל מה שהמדע יודע על אור. מדענים גילו תכונה מעניינת מאוד באור.

מסתבר שאיכשהו האור מתבטא כהתנהגות של זרם חלקיקים איכשהו.נמצא שהאנרגיה שנושא האור, לאחר ספירה על פני פרק זמן מסוים על ידי גלאי מיוחד, מסתבר שהיא מורכבת ממילא מחתיכות בודדות (שלמות).

לכן, הפך להיות נכון שאנרגיית האור היא בדידה, מכיוון שהיא מורכבת, כביכול, מחלקיקים בודדים - "קוואנטה", כלומר מחלקי האנרגיה השלמים הקטנים ביותר. חלקיק אור כזה, הנושא יחידה (או קוונטים) של אנרגיה, זכה לכינוי פוטון.

האנרגיה של פוטון אחד נמצאת בנוסחה הבאה:

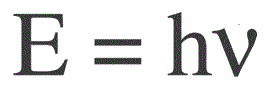
E — אנרגיית פוטון, h — קבוע של פלאנק, v — תדר.

הפיזיקאי הגרמני מקס פלאנק קבע לראשונה בניסוי את עובדת הדיסקרטיות של גל האור וחישב את ערכו של הקבוע h, המופיע בנוסחה למציאת האנרגיה של פוטונים בודדים. ערך זה התברר כ: 6.626 * 10-34 J * s. פלאנק פרסם את תוצאות עבודתו בסוף המאה ה-19.

שקול, למשל, קרן סגולה. התדר של אור כזה (f או v) הוא 7.5 * 1014 הרץ הקבוע של פלאנק (h) הוא 6.626 * 10-34 J * s. המשמעות היא שהאנרגיה של הפוטון, (E), האופיינית לצבע הסגול, היא 5*10-19 J. זהו חלק כל כך קטן של אנרגיה שקשה מאוד לתפוס אותו.

תארו לעצמכם נחל הררי - הוא זורם כיחידה אחת, ואי אפשר לראות בעין בלתי מזוינת שהנחל בעצם מורכב ממולקולות מים בודדות. היום, לעומת זאת, אנו יודעים שהאובייקט המקרוסקופי - הזרימה - הוא למעשה דיסקרטי, כלומר מורכב ממולקולות בודדות.

המשמעות היא שאם נוכל להציב מונה מולקולות ליד הזרם כדי לספור את מולקולות המים העוברות בזמן שהזרם זורם, הגלאי תמיד יספור רק מספרים שלמים של מולקולות מים, לא חלקיות.

באופן דומה, גרף האנרגיה הכוללת של הפוטון E, המחושב בזמן t - יתברר תמיד כלא ליניארי (איור צהוב), אלא בדרגה (איור ירוק):

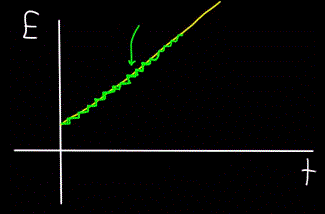
אז, פוטונים זזים, הם נושאים אנרגיה, ולכן יש להם מומנטום. אבל לפוטון אין מסה. איך אם כן אתה יכול למצוא מומנטום?

למעשה, עבור עצמים הנעים במהירויות הקרובות למהירות האור, הנוסחה הקלאסית p = mv פשוט אינה ישימה. כדי להבין כיצד למצוא מומנטום במקרה יוצא דופן זה, הבה נפנה לתורת היחסות הפרטית:

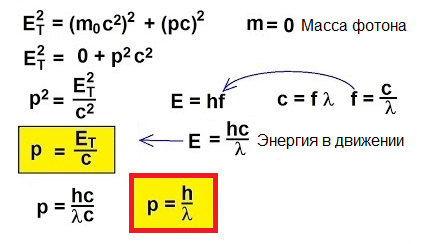
ב-1905 הסביר אלברט איינשטיין מנקודת מבט זו אפקט פוטואלקטרי... אנו יודעים שללוח המתכת יש אלקטרונים בתוכה, שבתוכה נמשכים הגרעינים הטעונים חיובית של האטומים ולכן נשמרים במתכת. אבל אם אתה מאיר צלחת כזו עם אור בתדר מסוים, אז אתה יכול להפיל אלקטרונים מהצלחת.

זה כאילו האור מתנהג כמו זרם של חלקיקים עם תנע, ולמרות שלפוטון אין מסה, הוא עדיין מקיים איכשהו אינטראקציה עם אלקטרון במתכת, ובתנאים מסוימים פוטון מסוגל לדפוק אלקטרון.

אז אם לפוטון שתקף על הלוח יש מספיק אנרגיה, אז האלקטרון יידפק מהמתכת ויצא מהלוח עם מהירות v. אלקטרון מופק כזה נקרא פוטואלקטרון.

מכיוון שלאלקטרון המופק יש מסה ידועה m, תהיה לו אנרגיה קינטית מסוימת mv.

אנרגיית הפוטון, כאשר היא פעלה על המתכת, מומרת לאנרגיית יציאת האלקטרון מהמתכת (פונקציית עבודה) ולאנרגיה הקינטית של האלקטרון, שבבעלותה האלקטרון המופק מתחיל לנוע מחוץ למתכת, עוזב אותה.

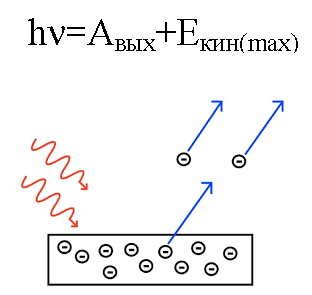
נניח שפוטון בעל אורך גל ידוע פוגע במשטח של מתכת שעבורה ידועה תפקוד העבודה (של אלקטרון מהמתכת). במקרה זה, ניתן למצוא בקלות את האנרגיה הקינטית של אלקטרון הנפלט ממתכת נתונה, כמו גם את מהירותו.

אם האנרגיה של הפוטון אינה מספיקה עבור האלקטרון לבצע את תפקיד העבודה, אז האלקטרון פשוט לא יכול לעזוב את פני המתכת הנתונה והפוטו-אלקטרון לא נוצר.

בשנת 1924, פיזיקאי צרפתי לואי דה ברולי העלה רעיון פורץ דרך לפיו לא רק פוטונים של אור אלא אלקטרונים עצמם יכולים להתנהג כמו גלים. המדען אפילו הסיק נוסחה עבור אורך הגל ההיפותטי של האלקטרון. גלים אלו כונו לאחר מכן "גלי דה ברולי".

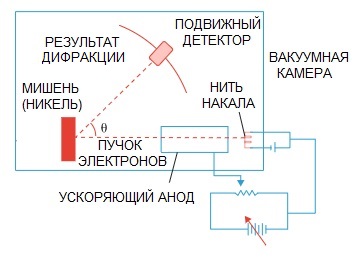
השערתו של דה ברולי אוששה מאוחר יותר. ניסוי פיזיקה על עקיפה של אלקטרונים, שנערך ב-1927 על ידי המדענים האמריקאים קלינטון דייוויסון ולסטר גרמר, הצביע לבסוף על אופי הגל של האלקטרון.

כאשר אלומת אלקטרונים הופנתה דרך מבנה אטומי מיוחד, נראה שהגלאי היה צריך לתעד את התמונה כחלקיקים שעפים בזה אחר זה, מה שהיה צפוי אם אלקטרונים היו חלקיקים.

אבל בפועל יש לנו תמונה האופיינית לעקירת גלים. יתרה מכך, אורכי הגלים הללו תואמים לחלוטין את הרעיון שהציע דה ברולי.

בסופו של דבר, הרעיון של דה ברולי איפשר להסביר את העיקרון של המודל האטומי של בוהר, ומאוחר יותר איפשר לארווין שרדינגר להכליל את הרעיונות הללו ולהניח את היסודות של פיזיקת הקוונטים המודרנית.