מהו כוח מגנטו-מוטיב, חוק הופקינסון

במחצית השנייה של המאה ה-19, הפיזיקאי האנגלי ג'ון הופקינסון ואחיו אדוארד הופקינסון, שפיתחו את התיאוריה הכללית של מעגלים מגנטיים, גזרו נוסחה מתמטית בשם "נוסחת הופקינסון" או חוק הופקינסון, שהיא אנלוגיה לחוק אוהם (בשימוש לחישוב מעגלים חשמליים).

לכן, אם החוק הקלאסי של אוהם מתאר מתמטית את הקשר בין זרם וכוח אלקטרו-מונע (EMF), חוק הופקינסון מבטא באופן דומה את הקשר בין השטף המגנטי לבין מה שנקרא כוח מגנוטומטיבי (MDF).

כתוצאה מכך, התברר שכן כוח מגנטו-מוטיבי הוא גודל פיזיקלי המאפיינת את יכולתם של זרמים חשמליים ליצור שטפים מגנטיים. וחוק הופקינסון בהקשר זה יכול לשמש בהצלחה בחישובים של מעגלים מגנטיים, שכן ה-MDF במעגלים מגנטיים הוא אנלוגי ל-EMF במעגלים חשמליים. תאריך הגילוי של חוק הופקינסון נחשב לשנת 1886.

גודל הכוח המגנטו-מוטיבי (MDF) נמדד בתחילה באמפר או, אם אנחנו מדברים על סליל עם זרם או אלקטרומגנט, אז לנוחיות החישובים השתמש בביטוי שלו בסיבובי אמפר:

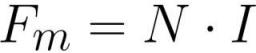
כאשר: Fm הוא הכוח המגנטו-מוטיבי בסליל [אמפר * סיבוב], N הוא מספר הסיבובים בסליל [סיבוב], I הוא כמות הזרם בכל אחד מהסיבובים של הסליל [אמפר].

אם תזין את ערך השטף המגנטי כאן, אז חוק הופקינסון עבור המעגל המגנטי יקבל את הצורה:

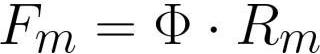
כאשר: Fm הוא הכוח המגנטו-מוטיבי בסליל [אמפר * סיבוב], F הוא השטף המגנטי [weber] או [henry * אמפר], Rm הוא ההתנגדות המגנטית של מוליך השטף המגנטי [אמפר * סיבוב / weber] או [ פנה / הנרי] .

הניסוח הטקסטואלי של חוק הופקינסון היה במקור כדלקמן: "במעגל מגנטי לא מסועף, השטף המגנטי עומד ביחס ישר לכוח המגנטו-מוטיב ויחס הפוך להתנגדות המגנטית הכוללת." כלומר, חוק זה קובע את הקשר בין כוח מגנטו-מוטיב, חוסר רצון ושטף מגנטי במעגל:

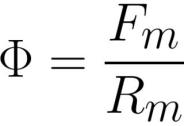
כאן: F הוא השטף המגנטי [וובר] או [הנרי * אמפר], Fm הוא הכוח המגנטו-מוטיבי בסליל [אמפר * סיבוב], Rm הוא ההתנגדות המגנטית של מוליך השטף המגנטי [אמפר * סיבוב / וובר] או [ פנה / הנרי] .

כאן חשוב לציין שלמעשה לכוח המגנטו-מוטיב (MDF) יש הבדל מהותי מהכוח האלקטרו-מוטיבי (EMF), המורכב מכך שאף חלקיק לא נע ישירות בשטף המגנטי, בעוד שהזרם הנובע בפעולת ה-EMF לוקח את התנועה של חלקיקים טעונים, למשל אלקטרונים בחוטי מתכת. עם זאת, הרעיון של MDS עוזר לפתור את הבעיות של חישוב מעגלים מגנטיים.

קחו למשל מעגל מגנטי לא מסועף הכולל עול של שטח חתך S, זהה לכל אורכו, ולחומר העול יש חדירות מגנטית mu.

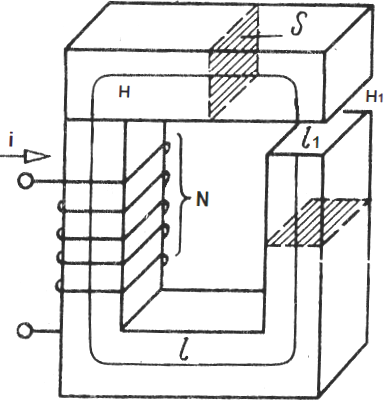
פער בעול - חומר שונה, חדירות מגנטית איזה mu1. הסליל המונח על העול מכיל N סיבובים, זרם i זורם בכל אחד מהסיבובים של הסליל. אנו מיישמים את משפט מחזור השדה המגנטי על קו המרכז של העול:

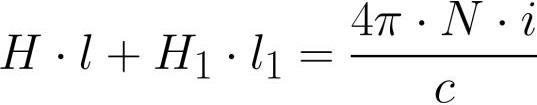
כאשר: H הוא עוצמת השדה המגנטי בתוך העול, H1 הוא עוצמת השדה המגנטי בתוך הפער, l הוא אורך קו המרכז של השראת העול (ללא הפער), l1 הוא אורך הפער.

מכיוון שלשטף המגנטי בתוך העול ובתוך הפער יש ערך זהה (בשל המשכיות קווי האינדוקציה המגנטיים), לאחר כתיבת Ф = BS ו-В = mu * H, נכתוב את עוצמת השדה המגנטי ביתר פירוט. , ולאחר החלפת זה בנוסחה שלמעלה:

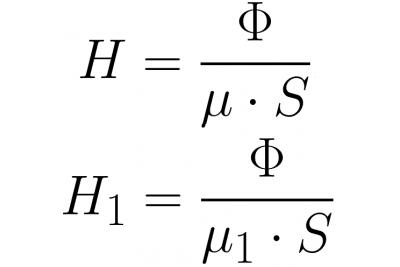
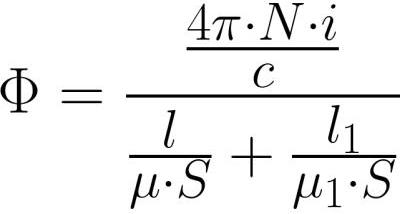
קל לראות שכמו ה-EMF בחוק אוהם למעגלים חשמליים, ה-MDS

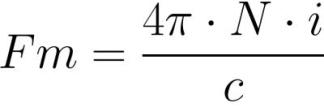
כאן ממלא את התפקיד של כוח אלקטרו-מוטיבי והתנגדות מגנטית

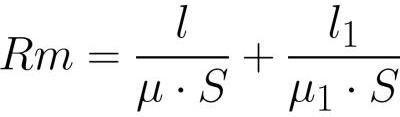
תפקיד ההתנגדות (באנלוגיה עם חוק אוהם הקלאסי).