חישוב פוטנציומטר ושאנט מורכב

מושגים ונוסחאות

פוטנציומטר הוא התנגדות משתנה עם סליידר הכלול כמתואר באיור.

לפרטים נוספים ראה - פוטנציומטרים ויישומים שלהם

מתח U מופעל על נקודות 1 ו-2. מתח מתכוונן מוסר מנקודות 2 ו-3, שערכו קטן מ-U ותלוי במיקום המחוון. למפרידי מתח יש סכימה דומה, אך הם אינם מתכווננים ואין להם מחוון נע.

פוטנציומטרים, מחלקי מתח ושאנטים מורכבים מחושבים באמצעות חוקי קירכהוף, כגון חישוב מעגלים קונבנציונליים עם התנגדויות.

דוגמאות של

1. מתח המקור הוא U = 24 V, ההתנגדות הכוללת של הפוטנציומטר היא r = 300 אוהם. המנוע מותקן בנפרד כך שr1 = 50 אוהם. איזה מתח U1 ניתן להסיר מנקודות 3 ו-2 (איור 1)?

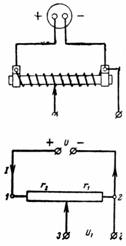
אורז. 1.

הזרם I והמתח U על פני ההתנגדות r קשורים בנוסחה I ∙ r = U.

מחוון הפוטנציומטר מפריד חלק מההתנגדות, כלומר. ההתנגדות r1. מפל המתח בין נקודות 3 ו-2 שווה ל-I ∙ r1 = U1.

מיחס מפל המתח נקבל את השוויון (I ∙ r1) / (I ∙ r) = U1 / U. ככל שההתנגדות r1 גדולה יותר, כך גדל הערך של המתח U1 בין נקודות 3 ל-2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. הפוטנציומטר (איור 2) נטען על מנורה עם התנגדות r = 100 אוהם. הפוטנציומטר מחולק על ידי מחוון לשני חלקים עם r1 = 600 אוהם ו-r2 = 200 אוהם. קבע את המתח Ul ואת זרם המנורה Il.

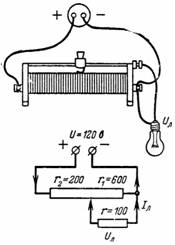
אורז. 2.

זרם I זורם דרך התנגדות r2 וזרם Il זורם דרך המנורה. זרם I-Il זורם דרך ההתנגדות r1, היוצר מתח על פני ההתנגדות r1 השווה למתח המנורה: (I-Il) ∙ r1 = Ul.

מצד שני, מתח המנורה שווה למתח המקור מינוס נפילת מתח בהתנגדות r2: U-I ∙ r2 = Ul.

הזרם I שווה למתח המקור חלקי ההתנגדות המתקבלת של החיבור הסדרתי-מקבילי של ההתנגדויות:

I = U / (r2 + (r ∙ r1) / (r + r1)).

נחליף את הביטוי בזרם הכולל של המקור במשוואה השנייה:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

לאחר השינוי, נקבל ביטוי למתח המנורה:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

אם נהפוך את הביטוי הזה, החל מהעובדה ש-Ul = Il ∙ r, אז נקבל ביטוי לזרם המנורה:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

החליפו את הערכים המספריים במשוואות המתקבלות:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul / r = 36/100 = 0.36 A.

3. חשב את המתח Up והזרם Ip של מכשיר המדידה המחובר לחלק מהפוטנציומטר. למכשיר התנגדות של r = 1000 אוהם. נקודת ההסתעפות מחלקת את ההתנגדות של המחלק ל-r2 = 500 אוהם ו-r1 = 7000 אוהם (איור 3).מתח במסופים של הפוטנציומטר U = 220 V.

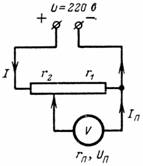
אורז. 3.

באמצעות הנוסחאות שהתקבלו קודם לכן, נוכל לכתוב שהזרם הזורם במכשיר הוא:

ב = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 010 0 = 010 500 = 000 500 1 = 010 1.54 / 11 = 0.14 א.

למעלה = Ip ∙ r = 0.14 ∙ 1000 = 14 V.

4. חשב את המתח של המכשיר Up, אם הוא צורך זרם Ip = 20 mA ומחובר לפוטנציומטר המחולק להתנגדויות r2 = 10 ^ 4 Ohm ו- r1 = 2 ∙ 10 ^ 4 Ohm (איור 3).

המתח הכולל במחלק המתח שווה לסכום נפילות המתח בחלקיו (דרך ההתנגדויות r1 ו-r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + למעלה

זרם המקור מסועף בנקודת המגע של המנוע: I = I1 + Ip; I = Upn / r1 + In.

נחליף את הערך של הזרם I במשוואת המתח:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

לכן, מתח המכשיר Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

החלף את הערכים המספריים: למעלה = (220-0.02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13.3 V.

5. מקור זרם ישר עם מתח U = 120 V מספק את מעגלי האנודה של מקלט הרדיו באמצעות פוטנציומטר (מחלק מתח), אשר יחד עם המסנן יש התנגדות של r = 10000 אוהם. המתח U1 מוסר על ידי ההתנגדות r2 = 8000 אוהם. חשב את מתח האנודה ללא עומס ובזרם עומס I = 0.02 A (איור 4).

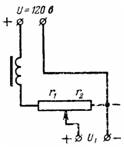
אורז. 4.

המקרה הראשון דומה לדוגמא 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

המקרה השני דומה לדוגמא 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0.02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

בעת הטעינה, המתח יירד מ-96 ל-64 וולט.אם יש צורך במתח נוסף, יש להזיז את המחוון שמאלה, כלומר, יש להגביר את ההתנגדות r2.

6. מתחי Ua ו-Ub מוסרים על ידי מחלק המתח. ההתנגדות הכוללת של מחלק המתח המחובר למתח U1 = 220 V היא r = 20,000 אוהם. מהו המתח Ua בהתנגדות r3 = 12000 אוהם עם צריכת זרם Ia = 0.01 A והמתח Ub בהתנגדות r2 + r3 = 18000 Ohm עם צריכת זרם Ib = 0.02 A (איור 5).

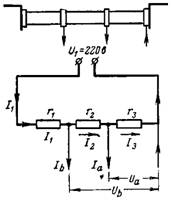
אורז. 5.

התנגדות מתח r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0.01 ∙ 8000-0.02 ∙ 2000) / 20,000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

המתח Ub שווה לסכום מפל המתח Ua על פני ההתנגדות r3 ומפל המתח על פני ההתנגדות r2. נפילת המתח על פני ההתנגדות r2 שווה ל-I2 ∙ r2. זרם I2 = Ia + I3. ניתן לחשב את הנוכחי I3 כמו בדוגמה 1:

I3 = (220-80-40) / 20,000 = 0.005 A;

I2 = Ia + I3 = 0.01 + 0.005 = 0.015 A.

מתח Ub = Ua + I2 ∙ r2 = 5 + 0.015 ∙ 6000 = 150 V.

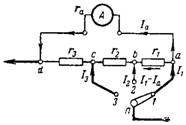
7. חשב את ה-shunt המשולב למיליאממטר כך שבמיקומים שונים של המתג יהיו לו טווחי המדידה הבאים: I1 = 10 mA; I2 = 30mA; I3 = 100mA. תרשים חיבור ה-shunt מוצג באיור. 6. התנגדות פנימית של המכשיר ra = 40 אוהם. טווח מדידה פנימי של מיליאממטר 2 mA.

אורז. 6.

בעת מדידת זרם I≤2mA, ה-shunt כבוי.

א) בעת מדידת הזרם I = 10 mA, המתג נמצא במצב 1 וזרם של 10-2 = 8 mA זורם דרך כל התנגדויות ה-shunt. ירידת המתח על פני התנגדות ה-shunt Ush והמכשיר Ua בין נקודות d ו-a חייבת להיות זהה

אוש = Ua;

(I1-Ia) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0.008 ∙ (r1 + r2 + r3) = 0.002 ∙ 40.

ב) בעת מדידת זרם I2 = 30 mA, המתג נמצא במצב 2. הזרם הנמדד יתחלק בנקודה b. בהטיה מלאה של המצביע של המכשיר, הזרם Ia = 2 mA יעבור דרך ההתנגדות r1 והמכשיר ra.

שאר הזרם I2-Ia יעבור דרך ההתנגדויות r2 ו-r3. הזרמים ייצרו את אותה מפל מתח על פני שני הענפים בין נקודות d ו-b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0.03-0.002) ∙ (r2 + r3) = 0.002 ∙ (r1 + 40).

ג) באופן דומה נבצע את החישוב בהגדלת טווח המדידה ל-I3 = 100 mA. זרם I3-Ia יזרום דרך התנגדות r3 וזרם Ia דרך התנגדות r1, r2, ra. המתח בשני הענפים זהה: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0.098 ∙ r3 = 0.002 ∙ (r1 + r2 + 40).

השגנו שלוש משוואות עם שלושה ערכים לא ידועים של התנגדויות r1, r2 ו-r3.

נכפיל את כל המשוואות ב-1000 ונמיר אותן:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

נוסיף את המשוואה הראשונה והשלישית: 50 ∙ r3 = 50;

r3 = 50/50 = 1 אוהם.

נוסיף את המשוואה הראשונה והשנייה: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2.34 אוהם.

בוא נחליף את התוצאות שהתקבלו במשוואה הראשונה: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6.66 אוהם.

ניתן לבדוק את נכונות החישוב על ידי החלפת ערכי ההתנגדות שהתקבלו במשוואות.