חישובים לשיפור מקדם ההספק ברשת תלת פאזית

בעת חישוב הקיבול של קבל לשיפור מקדם ההספק ברשת תלת פאזית, נקפיד על אותו רצף כמו במאמר עם דוגמאות לחישובים ברשת חד פאזית... הערך של גורם ההספק נקבע על ידי נוסחת ההספק עבור זרם תלת פאזי:

P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).

דוגמאות של

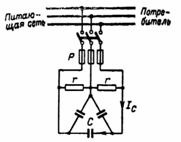
1. למנוע אינדוקציה תלת פאזי יש את נתוני הפאנל הבאים: P = 40 קילוואט, U = 380 V, I = 105 A, η = 0.85, f = 50 הרץ. חיבור כוכב של הסטטור. נניח שקשה לקבוע את ערך ה-cosφ של הלוח, ולכן יש צורך לקבוע אותו. לאיזה ערך יקטן הזרם לאחר שיפור מקדם ההספק ל-cosφ = 1 באמצעות קבלים? איזו קיבולת צריכה להיות הקבלים? על איזה כוח תגובתי יפצו הקבלים (איור 1)?

המלחציים של מתפתל הסטטור מסומנים: התחלה - C1, C2, C3, מסתיים - C4, C5, C6, בהתאמה.עם זאת, בהמשך, כדי להקל על התקשורת עם הדיאגרמות, המקור יסומן A, B, C והקצוות X, Y, Z.

אורז. 1.

הספק מנוע P1 = P2 / η = 40000 / 0.85 ≈47000 W,

כאשר P2 הוא ההספק הנקי המופיע על לוחית השם של המנוע.

cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0.69.

לאחר שיפור מקדם ההספק ל-cosφ = 1, הספק המבוא יהיה:

P1 = √3 ∙ U ∙ I ∙ 1

והזרם יירד ל

I1 = P1 / (√3 ∙ U) = 47000 / (1.73 ∙ 380) = 71.5 A.

זהו הזרם הפעיל ב-cosφ = 0.69 מאז

Ia = I ∙ cosφ = 105 ∙ 0.69 = 71.5 A.

באיור. 1 מראה הכללת קבלים לשיפור cosφ.

מתח קבלים Uph = U / √3 = 380 / √3 = 220 V.

זרם הממגנט הפאזי שווה לזרם הממגנט הליניארי: IL = I ∙ sinφ = 105 ∙ 0.75 = 79.8 A.

ההתנגדות הקיבולית של הקבל, שחייבת לספק את הזרם הממגנט, תהיה: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).

לכן, הקיבול של הקבל C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79.8 / (220 ∙ 3.14 ∙ 100) = 79.800 / (22 ∙ 3.14) ∙ 16.0 = (μ 16.0) ∙ 16.0

גוש קבלים בקיבולת כוללת של C = 3 ∙ 1156.4≈3469 μF חייב להיות מחובר למנוע תלת פאזי כדי לשפר את מקדם ההספק ל-cosφ = 1 ובמקביל להפחית את הזרם מ-105 ל-71.5 A.

הכוח התגובתי הכולל פיצוי על ידי קבלים, שבהיעדר קבלים נלקח מהרשת, Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79.8≈52668 = 52.66 kvar.

במקרה זה, המנוע צורך כוח פעיל P1 = 47 קילוואט רק מהרשת.

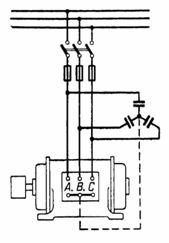
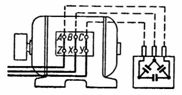
באיור.2 מציג בלוק של קבלים המחוברים בדלתא ומחוברים לטרמינלים של מנוע תלת פאזי שגם הפיתול שלו מחובר בדלתא. חיבור זה של קבלים הוא יתרון יותר מהחיבור המוצג באיור. 1 (ראה מסקנת חישוב 2).

אורז. 2.

2. תחנת כוח קטנה מזינה רשת תלת פאזית עם זרם I = 250 A במתח רשת U = 380 V ומקדם הספק רשת cosφ = 0.8. השיפור של גורם ההספק מושג על ידי קבלים המחוברים בדלתא לפי התרשים באיור. 3. יש צורך לקבוע את ערך הקיבול של הקבלים ואת ההספק התגובתי המתוגמל.

אורז. 3.

הספק לכאורה S = √3 ∙ U ∙ I = 1.73 ∙ 380 ∙ 250 = 164.3 kVA.

קבע את ההספק הפעיל ב-cosφ = 0.8:

P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164.3 ∙ 0.8 = 131.5 W.

כוח תגובתי לפיצוי ב-cosφ = 0.8

Q = S ∙ sinφ≈164.3 ∙ 0.6 = 98.6 kvar.

לכן, זרם המגנט הליניארי (איור 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.

זרם פאזה מגנט (קיבולי) ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86.5 A.

ניתן לקבוע את זרם הקבלים בדרך אחרת על ידי הזרם הממגנט (תגובתי) במעגל:

IL = I ∙ sinφ = 250 ∙ 0.6 = 150 A,

ICph = ILph = IL / √3 = 150 / 1.73 = 86.7 A.

כאשר מחוברים בדלתא, לכל קבוצת קבלים יש מתח של 380 וולט וזרם פאזה ICph = 86.7 A.

I = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.

לכן, C = IC / (U ∙ 2 ∙ π ∙ f) = 86.7 / (300 ∙ π ∙ 100) = 726 μF.

הקיבול הכולל של בנק הקבלים הוא C3 = 3 ∙ 726 = 2178 μF.

הקבלים המחוברים מאפשרים להשתמש בכל ההספק של תחנת הכוח S = 164.3 kVA בצורה של הספק נטו.ללא קבלי פעולה, רק הספק פעיל של 131.5 קילוואט משמש ב-cosφ = 0.8.

ההספק התגובתי המפוצה Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 גדל ביחס לריבוע המתח. לכן, הקיבולת הנדרשת של הקבלים, ומכאן גם עלות הקבלים, נמוכה יותר מכיוון שהמתח גבוה יותר.

התנגדויות r באיור. 3 משמשים לפירוק הדרגתי של קבלים כאשר הם מנותקים מהרשת.