התנגדויות, מוליכות ומעגלים שווים של שנאים ושנאים אוטומטיים

שנאי עם שתי פיתולים יכול להיות מיוצג על ידי מעגל שווה ערך בצורת T (איור 1, א), כאשר rt ו-xt הם ההתנגדות הפעילה והאינדוקטיבית של הפיתולים, gt היא המוליכות הפעילה עקב אובדן הספק פעיל בשנאי פלדה, bt היא ההולכה האינדוקטיבית עקב הזרם הממגנט...

הזרם בהולכה של השנאי קטן מאוד (בסדר גודל של כמה אחוזים מהזרם הנקוב שלו), לכן, בחישוב רשתות חשמליות בעלות משמעות אזורית, נעשה בדרך כלל שימוש במעגל שווה ערך עם שנאי בצורת L, שבו ההולכה מתווספת לטרמינלים של פיתול השנאי הראשוני (איור 1, ב) - לפיתול המתח הגבוה עבור שנאים יורדים ולפיתול המתח הנמוך עבור שנאים עולים. השימוש בתוכנית בצורת L מפשט את החישובים של רשתות חשמל.

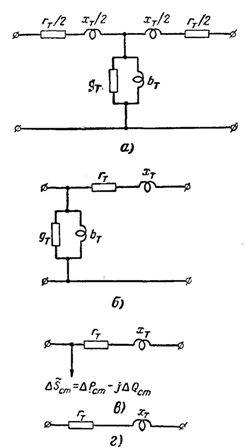
אורז. 1.מעגלים שווים של שנאי עם שני פיתולים: מעגל בצורת a-T; ב - תכנית בצורת G; ג - תוכנית פשוטה בצורת L לחישוב רשתות אזוריות; ד - תוכנית פשוטה לחישוב רשתות מקומיות ולחישוב משוער של רשתות אזוריות.

החישוב הוא אפילו פשוט יותר אם המוליכות של השנאי מוחלפת בעומס קבוע (איור 1, ג) השווה להספק ללא עומס של השנאי:

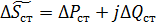
כאן ΔPCT - הפסדי הספק בפלדה שווים להפסדים במהלך פעולת ללא עומס של השנאי, ו-ΔQST - כוח מגנט של השנאי שווה ל:

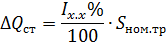
כאשר Ix.x% הוא זרם ללא עומס של השנאי כאחוז מהזרם הנקוב שלו; Snom.tr - הספק מדורג של השנאי.

עבור רשתות מקומיות n, בחישובים משוערים של רשתות אזוריות, רק ההתנגדות הפעילה והאינדוקטיבית של שנאים נלקחת בחשבון (איור 1, ד).

ההתנגדות הפעילה של הפיתולים של שנאי דו-מתפתלי נקבעת על ידי הפסדי ההספק הידועים בנחושת (בפיתולים) של השנאי ΔPm kW בעומס הנקוב שלו:

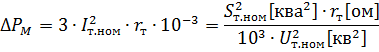
איפה

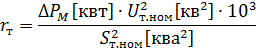
בחישובים מעשיים, ההנחה היא שהפסדי ההספק בנחושת (בפיתולים) של שנאי בעומס הנקוב שלו שווים להפסדי הקצר בזרם הנקוב של השנאי, כלומר. ΔPm ≈ ΔPk.

הכרת מתח הקצר uk% של השנאי, שווה מספרית למפל המתח בפיתוליו בעומס נקוב, מבוטא כאחוז מהמתח הנקוב שלו, כלומר.

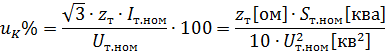
ניתן לקבוע את העכבה של פיתולי השנאי

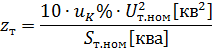
ולאחר מכן ההתנגדות האינדוקטיבית של פיתולי השנאי

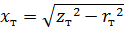
עבור שנאים גדולים עם התנגדות נמוכה מאוד, ההתנגדות האינדוקטיבית ניתנת בדרך כלל על ידי המצב המשוער הבא:

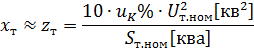
בעת שימוש בנוסחאות החישוב, יש לזכור שניתן לקבוע את ההתנגדויות של פיתולי השנאי במתח הנקוב של הפיתולים הראשוניים והמשניים שלו. בחישובים מעשיים, נוח יותר לקבוע rt ו-xt במתח הנומינלי של הפיתול שעבורו נעשה החישוב.

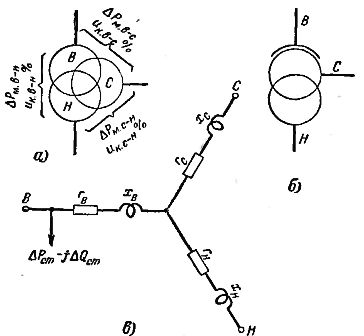
אורז. 2... מעגלי שנאי עם שלוש פיתולים ושנאים אוטומטיים: א - דיאגרמה של שנאי עם שלוש פיתולים; ב - מעגל שנאי אוטומטי; ג - מעגל שווה ערך של שנאי עם שלוש פיתולים ושנאי אוטומטי.

אם לפיתול השנאי יש מספר מתכוונן של סיבובים, אזי Ut.nom נלקח כפלט של הפיתול הראשי.

רובוטריקים עם שלוש פיתולים (איור 2, א) ושנאים אוטומטיים (איור 2, ב) מאופיינים בערכים של הפסדי כוח ΔРm = ΔРк. ומתחי קצר ir% עבור כל זוג פיתולים:

ΔPk. c-s, ΔPk. vn, ΔPk. s-n

ו

ik.v-s, ℅, ik.v-n, ℅, ik. s-n, ℅,

מופחת להספק הנקוב של השנאי או השנאי האוטומטי. הכוח הנומינלי של האחרון שווה לכוח המעבר שלו. המעגל המקביל של שנאי תלת מתפתל או שנאי אוטומטי מוצג באיור. 2, v.

הפסדי הכוח ומתח הקצר הקשורים לקרניים בודדות של כוכב שווה ערך של מעגל שווה ערך נקבעים על ידי הנוסחאות:

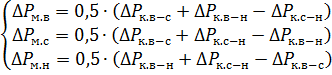
ו

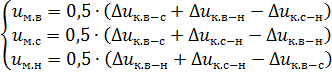
ההתנגדות הפעילה והאינדוקטיבית של קרני הכוכב השקול של המעגל המקביל נקבעות מהנוסחאות של שנאים דו-פתיליים, ומחליפות לתוכם את ערכי אובדן הכוח ומתח הקצר עבור הקרן המתאימה של הכוכב השקול. של המעגל המקביל.