אלקטרון בשדה חשמלי
תנועת האלקטרון בשדה חשמלי היא אחד התהליכים הפיזיקליים החשובים ביותר להנדסת חשמל. דמות בוא נראה איך זה קורה בחלל ריק. הבה נבחן תחילה דוגמה לתנועה של אלקטרון מהקתודה לאנודה בשדה חשמלי אחיד.
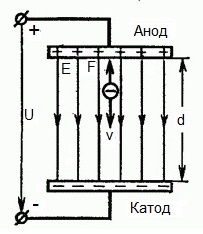
האיור שלהלן מציג מצב שבו אֶלֶקטרוֹן יוצא מהאלקטרודה השלילית (קתודה) עם מהירות התחלתית קטנה באופן זניח (שואף לאפס) ונכנס בשדה חשמלי אחידקיים בין שתי אלקטרודות.
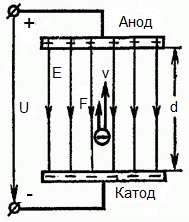
מתח קבוע U מופעל על האלקטרודות, ולשדה החשמלי יש חוזק תואם E. המרחק בין האלקטרודות שווה ל-d. במקרה זה, יפעל על האלקטרון כוח F מצד השדה, שהוא פרופורציונלי למטען האלקטרון ולחוזק השדה:
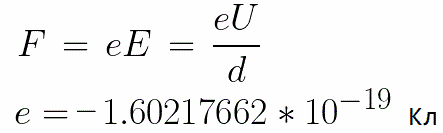
מכיוון שלאלקטרון יש מטען שלילי, כוח זה יופנה כנגד וקטור חוזק השדה E. בהתאם לכך, האלקטרון יואץ בכיוון זה על ידי השדה החשמלי.
התאוצה שחווה האלקטרון היא פרופורציונלית לגודל הכוח F הפועל עליו ופרופורציונלית הפוך למסת האלקטרון m.מכיוון שהשדה אחיד, התאוצה עבור תמונה נתונה יכולה להתבטא כך:
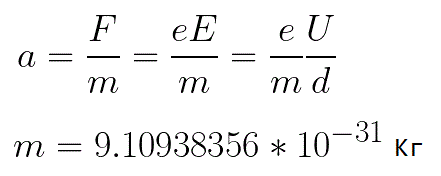
בנוסחה זו, היחס בין מטען האלקטרון למסה שלו הוא המטען הספציפי של האלקטרון, כמות שהיא קבועה פיזיקלית:
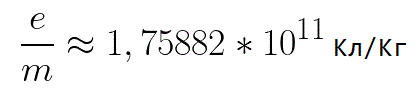
אז האלקטרון נמצא בשדה חשמלי מואץ מכיוון שכיוון המהירות ההתחלתית v0 עולה בקנה אחד עם כיוון הכוח F בצד השדה ולכן האלקטרון נע בצורה אחידה. אם אין מכשולים, הוא יעבור בנתיב d בין האלקטרודות ויגיע לאנודה (אלקטרודה חיובית) במהירות מסוימת v. ברגע שהאלקטרון מגיע לאנודה, האנרגיה הקינטית שלו תהיה שווה בהתאמה ל:
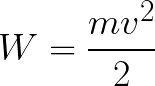
מכיוון שלאורך כל הנתיב d האלקטרון מואץ על ידי כוחות השדה החשמלי, הוא רוכש אנרגיה קינטית זו כתוצאה מהעבודה שנעשה על ידי הכוח הפועל בצד השדה. עבודה זו שווה ל:
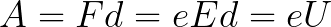
אז ניתן למצוא את האנרגיה הקינטית שנרכשת על ידי האלקטרון שנע בשדה באופן הבא:
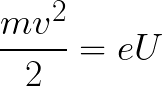
כלומר, זה לא יותר מעבודתם של כוחות שדה להאיץ אלקטרון בין נקודות עם הפרש פוטנציאל U.
במצבים כאלה, כדי לבטא את האנרגיה של אלקטרון, נוח להשתמש ביחידת מדידה כזו כמו "וולט האלקטרון", ששווה לאנרגיה של אלקטרון במתח של 1 וולט. ומכיוון שמטען האלקטרונים קבוע, אז 1 אלקטרו-וולט הוא גם ערך קבוע:
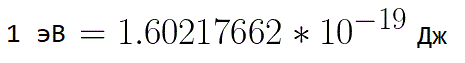
מהנוסחה הקודמת, אתה יכול לקבוע בקלות את מהירות האלקטרון בכל נקודה בנתיבו כאשר הוא נע בשדה חשמלי מואץ, לדעת רק את הפרש הפוטנציאל שהוא עבר בעת האצה:
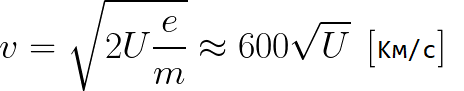
כפי שאנו יכולים לראות, מהירותו של אלקטרון בשדה מאיץ תלויה רק בהפרש הפוטנציאל U בין נקודת הסיום לנקודת ההתחלה של דרכו.
תארו לעצמכם שהאלקטרון מתחיל להתרחק מהקתודה במהירות זניחה, והמתח בין הקתודה לאנודה הוא 400 וולט. במקרה זה, ברגע ההגעה לאנודה, המהירות שלה תהיה שווה ל:
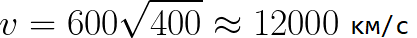
קל גם לקבוע את הזמן הדרוש לאלקטרון לעבור את המרחק d בין האלקטרודות. עם תנועה מואצת אחידה ממנוחה, נמצא שהמהירות הממוצעת היא מחצית מהמהירות הסופית, ואז זמן הטיסה המואצת בשדה חשמלי יהיה שווה ל:
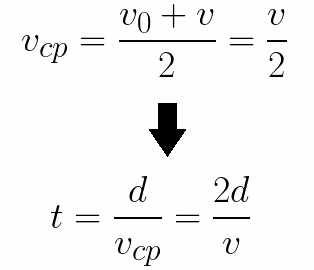
הבה נבחן כעת דוגמה כאשר אלקטרון נע בשדה חשמלי אחיד מאט, כלומר, השדה מכוון כמו קודם, אך האלקטרון מתחיל לנוע בכיוון ההפוך - מהאנודה לקתודה.
נניח שהאלקטרון עזב את האנודה עם מהירות התחלתית כלשהי v ובהתחלה התחיל לנוע בכיוון הקתודה. במקרה זה, הכוח F הפועל על האלקטרון מהצד של השדה החשמלי יופנה כנגד וקטור העוצמה החשמלי E - מהקתודה לאנודה.
הוא יתחיל להפחית את המהירות ההתחלתית של האלקטרון, כלומר השדה יאט את האלקטרון. המשמעות היא שהאלקטרון בתנאים אלו יתחיל לנוע בצורה אחידה ואחידה באיטיות. המצב מתואר כך: "אלקטרון נע בשדה חשמלי מאט".
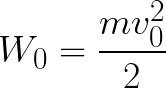
מהאנודה החל האלקטרון לנוע באנרגיה קינטית שאינה אפס, שמתחילה לרדת במהלך ההאטה, מאחר שהאנרגיה מושקעת כעת בהתגברות על הכוח הפועל מהשדה על האלקטרון.
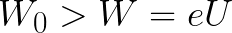
אם האנרגיה הקינטית הראשונית של האלקטרון בעת יציאתו מהאנודה הייתה גדולה מידית מהאנרגיה שהשדה חייב להוציא כדי להאיץ את האלקטרון במעבר מהקתודה לאנודה (כמו בדוגמה הראשונה), אז האלקטרון היה לעבור מרחק d ובסופו של דבר יגיע לקתודה למרות בלימה.
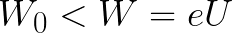
אם האנרגיה הקינטית הראשונית של האלקטרון קטנה מהערך הקריטי הזה, אזי האלקטרון לא יגיע לקתודה. בשלב מסוים הוא ייעצר, ואז תתחיל תנועה מואצת אחידה בחזרה לאנודה. כתוצאה מכך השדה יחזיר לו את האנרגיה שהושקעה בתהליך העצירה.
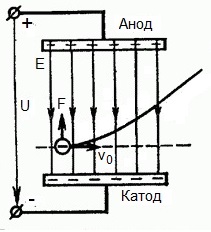
אבל מה אם אלקטרון עף במהירות v0 באזור הפעולה של שדה חשמלי בזווית ישרה? ברור שהכוח בצד השדה באזור זה מופנה עבור האלקטרון מהקתודה לאנודה, כלומר כנגד וקטור חוזק השדה החשמלי E.
המשמעות היא שכעת יש לאלקטרון שני מרכיבי תנועה: הראשון - עם מהירות v0 בניצב לשדה, השני - מואץ באופן אחיד תחת פעולת הכוח מצד השדה המכוון לאנודה.
מסתבר שלאחר שטס לשדה הפעולה, האלקטרון נע לאורך מסלול פרבולי. אבל לאחר טיסה מחוץ לאזור הפעולה של השדה, האלקטרון ימשיך בתנועתו האחידה על ידי אינרציה לאורך מסלול קו ישר.

